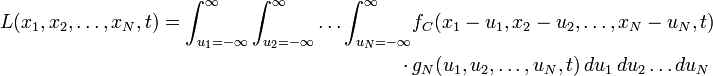Scale Space Implementation

Scale Space Implementation

The linear scale-space representation of an N-dimensional continuous signal is obtained by convolving with an N-dimensional Gaussian kernel

\begin{align} L(x_1, x_2, \dots, x_N, t) = \int_{u_1=-\infty}^{\infty} \int_{u_2=-\infty}^{\infty} \dots \int_{u_N=-\infty}^{\infty} &f_C(x_1-u_1, x_2-u_2, \dots, x_N-u_N, t)\\ \, \cdot \, &g_N(u_1, u_2, \dots, u_N, t) \, du_1 \, du_2 \dots du_N \end{align}

However, for implementation, this definition is impractical, since it is continuous. When applying the scale space concept to a discrete signal, different approaches can be taken. This article is a brief summary of some of the most frequently used methods.

Read more about Scale Space Implementation:  Separability, The Sampled Gaussian Kernel, The Discrete Gaussian Kernel, Recursive Filters, Finite-impulse-response (FIR) Smoothers, Real-time Implementation Within Pyramids and Discrete Approximation of Scale-normalized Derivatives, Other Multi-scale Approaches, See Also

Famous quotes containing the words scale and/or space:

    “With a defeated joy,
    With an auspicious, and a dropping eye,
    With mirth in funeral, and with dirge in marriage,
    In equal scale weighing delight and dole.”
    —William Shakespeare (1564–1616)

    “The within, all that inner space one never sees, the brain and the heart and other caverns where thought and feeling dance their sabbath.”
    —Samuel Beckett (1906–1989)