Rotation Matrix - in Two Dimensions

In Two Dimensions

In two dimensions every rotation matrix has the following form:

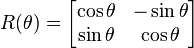$R(\theta) = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{bmatrix}$ .

This rotates column vectors by means of the following matrix multiplication:

$\begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ \end{bmatrix}$ .

So the coordinates (x',y') of the point (x,y) after rotation are:

The direction of vector rotation is counterclockwise if θ is positive (e.g. 90°), and clockwise if θ is negative (e.g. -90°).

$R(-\theta) = \begin{bmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \\ \end{bmatrix}\,$ .

Note that the two-dimensional case is the only non-trivial (e.g. one dimension) case where the rotation matrices group is commutative, so that it does not matter the order in which multiple rotations are performed.

Read more about this topic: Rotation Matrix

Famous quotes containing the word dimensions:

“Is it true or false that Belfast is north of London? That the galaxy is the shape of a fried egg? That Beethoven was a drunkard? That Wellington won the battle of Waterloo? There are various degrees and dimensions of success in making statements: the statements fit the facts always more or less loosely, in different ways on different occasions for different intents and purposes.”
—J.L. (John Langshaw)