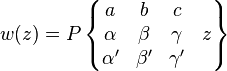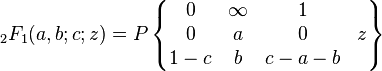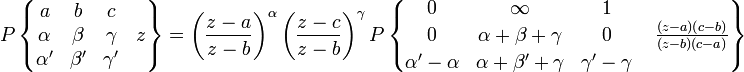Riemann's Differential Equation - Solutions

Solutions

The solutions are denoted by the Riemann P-symbol

w(z)=P \left\{ \begin{matrix} a & b & c & \; \\ \alpha & \beta & \gamma & z \\ \alpha' & \beta' & \gamma' & \; \end{matrix} \right\}

The standard hypergeometric function may be expressed as

\;_2F_1(a,b;c;z) = P \left\{ \begin{matrix} 0 & \infty & 1 & \; \\ 0 & a & 0 & z \\ 1-c & b & c-a-b & \; \end{matrix} \right\}

The P-functions obey a number of identities; one of them allows a general P-function to be expressed in terms of the hypergeometric function. It is

P \left\{ \begin{matrix} a & b & c & \; \\ \alpha & \beta & \gamma & z \\ \alpha' & \beta' & \gamma' & \; \end{matrix} \right\} = \left(\frac{z-a}{z-b}\right)^\alpha \left(\frac{z-c}{z-b}\right)^\gamma P \left\{ \begin{matrix} 0 & \infty & 1 & \; \\ 0 & \alpha+\beta+\gamma & 0 & \;\frac{(z-a)(c-b)}{(z-b)(c-a)} \\ \alpha'-\alpha & \alpha+\beta'+\gamma & \gamma'-\gamma & \; \end{matrix} \right\}

In other words, one may write the solutions in terms of the hypergeometric function as

w(z)= \left(\frac{z-a}{z-b}\right)^\alpha \left(\frac{z-c}{z-b}\right)^\gamma \;_2F_1 \left( \alpha+\beta +\gamma, \alpha+\beta'+\gamma; 1+\alpha-\alpha'; \frac{(z-a)(c-b)}{(z-b)(c-a)} \right)

The full complement of Kummer's 24 solutions may be obtained in this way; see the article hypergeometric differential equation for a treatment of Kummer's solutions.

Read more about this topic:  Riemann's Differential Equation

Famous quotes containing the word solutions:

    “Every man is in a state of conflict, owing to his attempt to reconcile himself and his relationship with life to his conception of harmony. This conflict makes his soul a battlefield, where the forces that wish this reconciliation fight those that do not and reject the alternative solutions they offer. Works of art are attempts to fight out this conflict in the imaginative world.”
    —Rebecca West (1892–1983)

    “The anorexic prefigures this culture in rather a poetic fashion by trying to keep it at bay. He refuses lack. He says: I lack nothing, therefore I shall not eat. With the overweight person, it is the opposite: he refuses fullness, repletion. He says, I lack everything, so I will eat anything at all. The anorexic staves off lack by emptiness, the overweight person staves off fullness by excess. Both are homeopathic final solutions, solutions by extermination.”
    —Jean Baudrillard (b. 1929)

    “Those great ideas which come to you in your sleep just before you awake in morning, those solutions to the world’s problems which, in the light of day, turn out to be duds of the puniest order, couldn’t they be put to some use, after all?”
    —Robert Benchley (1889–1945)