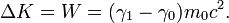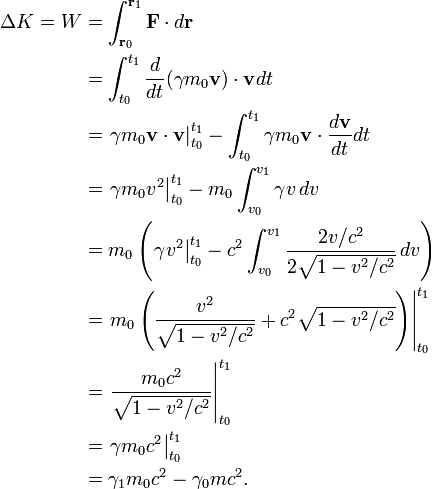Relativistic Mechanics - Kinetic Energy

Kinetic Energy

The work-energy theorem says the change in kinetic energy is equal to the work done on the body. In special relativity:

\begin{align} \Delta K = W = (\gamma_1 - \gamma_0) m_0c^2.\end{align}
Derivation
\begin{align} \Delta K = W &= \int_{\mathbf{r}_0}^{\mathbf{r}_1} \mathbf{F} \cdot d\mathbf{r} \\ &= \int_{t_0}^{t_1} \frac{d}{dt}(\gamma m_0 \mathbf{v})\cdot\mathbf{v}dt \\ &= \left. \gamma m_0 \mathbf{v} \cdot \mathbf{v} \right|^{t_1}_{t_0} - \int_{t_0}^{t_1} \gamma m_0\mathbf{v} \cdot \frac{d\mathbf{v}}{dt} dt \\ &= \left. \gamma m_0 v^2 \right|^{t_1}_{t_0} - m_0\int_{v_0}^{v_1} \gamma v\,dv \\ &= m_0 \left( \left. \gamma v^2 \right|^{t_1}_{t_0} - c^2\int_{v_0}^{v_1} \frac{2v/c^2}{2\sqrt{1-v^2/c^2}}\,dv \right) \\ &= \left. m_0\left(\frac {v^2}{\sqrt{1-v^2/c^2}} + c^2 \sqrt{1-v^2/c^2} \right) \right|^{t_1}_{t_0} \\ &= \left. \frac {m_0c^2}{\sqrt{1-v^2/c^2}} \right|^{t_1}_{t_0} \\ &= \left. {\gamma m_0c^2}\right|^{t_1}_{t_0} \\ &= \gamma_1 m_0c^2 - \gamma_0 mc^2.\end{align}

If in the initial state the body was at rest (γ0 = 1) and in the final state it has speed v (γ1 = γ), the kinetic energy is

a result that can be directly obtained by subtracting the rest energy m0c2 from the total relativistic energy γm0c2.

Read more about this topic:  Relativistic Mechanics

Famous quotes containing the words kinetic and/or energy:

    “The poem has a social effect of some kind whether or not the poet wills it to have. It has kinetic force, it sets in motion ... [ellipsis in source] elements in the reader that would otherwise be stagnant.”
    —Denise Levertov (b. 1923)

    “Much of the modern resistance to chastity comes from men’s belief that they “own” their bodies—those vast and perilous estates, pulsating with the energy that made the worlds, in which they find themselves without their consent and from which they are ejected at the pleasure of Another!”
    —C.S. (Clive Staples)