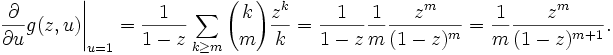Random Permutation Statistics - Probability That A Random Subset of Lies On The Same Cycle

Probability That A Random Subset of Lies On The Same Cycle

Select a random subset Q of containing m elements and a random permutation, and ask about the probability that all elements of Q lie on the same cycle. This is another average parameter. The function b(k) is equal to, because a cycle of length k contributes subsets of size m, where for k < m. This yields

\frac{\partial}{\partial u} g(z, u) \Bigg|_{u=1} = \frac{1}{1-z} \sum_{k\ge m} {k \choose m} \frac{z^k}{k} = \frac{1}{1-z} \frac{1}{m} \frac{z^m}{(1-z)^m} = \frac{1}{m} \frac{z^m}{(1-z)^{m+1}}.

Averaging out we obtain that the probability of the elements of Q being on the same cycle is

{n \choose m}^{-1} \frac{1}{m} \frac{z^m}{(1-z)^{m+1}} = {n \choose m}^{-1} \frac{1}{m} \frac{1}{(1-z)^{m+1}}

or

\frac{1}{m} {n \choose m}^{-1} {(n-m) \; + \; m \choose m} = \frac{1}{m}.

In particular, the probability that two elements p < q are on the same cycle is 1/2.

Read more about this topic:  Random Permutation Statistics

Famous quotes containing the words probability, random, lies and/or cycle:

    “Only in Britain could it be thought a defect to be “too clever by half.” The probability is that too many people are too stupid by three-quarters.”
    —John Major (b. 1943)

    “It is a secret from nobody that the famous random event is most likely to arise from those parts of the world where the old adage “There is no alternative to victory” retains a high degree of plausibility.”
    —Hannah Arendt (1906–1975)

    “This be the verse you grave for me:
    Here he lies where he longed to be;
    Home is the sailor, home from the sea,
    And the hunter home from the hill.”
    —Robert Louis Stevenson (1850–1894)

    “Only mediocrities progress. An artist revolves in a cycle of masterpieces, the first of which is no less perfect than the last.”
    —Oscar Wilde (1854–1900)