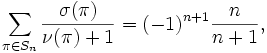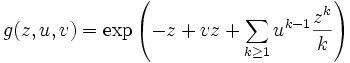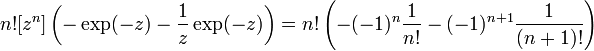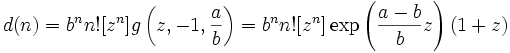Random Permutation Statistics - A Problem From The 2005 Putnam Competition

A Problem From The 2005 Putnam Competition

A link to the Putnam competition website appears in the section External links. The problem asks for a proof that

$\sum_{\pi\in S_n} \frac{\sigma(\pi)}{\nu(\pi)+1} = (-1)^{n+1} \frac{n}{n+1},$

where the sum is over all permutations of, is the sign of, i.e. if is even and if is odd, and is the number of fixed points of .

Now the sign of is given by

where the product is over all cycles c of, as explained e.g. on the page on even and odd permutations.

Hence we consider the combinatorial class

$\mathfrak{P}( - \mathcal{Z} + \mathcal{V} \mathcal{Z} + \mathfrak{C}_1(\mathcal{Z}) + \mathcal{U}\mathfrak{C}_2(\mathcal{Z}) + \mathcal{U}^2\mathfrak{C}_3(\mathcal{Z}) + \mathcal{U}^3\mathfrak{C}_4(\mathcal{Z}) + \cdots)$

where marks one minus the length of a contributing cycle, and marks fixed points. Translating to generating functions, we obtain

$g(z, u, v) = \exp\left( -z + vz + \sum_{k\ge 1} u^{k-1} \frac{z^k}{k} \right)$

$\exp\left( -z + vz + \frac{1}{u} \log\frac{1}{1-uz} \right) = \exp(-z + vz) \left(\frac{1}{1-uz} \right)^{1/u}.$

Now we have

$n! g(z, -1, v) = n! \exp(-z + vz) (1 + z) = \sum_{\pi\in S_n} \sigma(\pi) v^{\nu(\pi)}$

and hence the desired quantity is given by

$n! \int_0^1 g(z, -1, v) dv = \sum_{\pi\in S_n} \frac{\sigma(\pi)}{\nu(\pi)+1}.$

Doing the computation, we obtain

$\int_0^1 g(z, -1, v) dv = \exp(-z)(1+z) \left(\frac{1}{z}\exp(z) - \frac{1}{z}\right)$

$\left(\frac{1}{z} + 1\right) \left(1 - \exp(-z)\right) = \frac{1}{z} + 1 - \exp(-z) - \frac{1}{z} \exp(-z).$

Extracting coefficients, we find that the coefficient of is zero. The constant is one, which does not agree with the formula (should be zero). For positive, however, we obtain

$n! \left( - \exp(-z) - \frac{1}{z} \exp(-z) \right) = n! \left( - (-1)^n \frac{1}{n!} - (-1)^{n+1} \frac{1}{(n+1)!} \right)$

$(-1)^{n+1} \left( 1 - \frac{1}{n+1} \right) = (-1)^{n+1} \frac{n}{n+1},$

which is the desired result.

As an interesting aside, we observe that may be used to evaluate the following determinant of an matrix:

$d(n) = \det(A_n) = \begin{vmatrix} a && b && b && \cdots && b \\ b && a && b && \cdots && b \\ b && b && a && \cdots && b \\ \vdots && \vdots && \vdots && \ddots && \vdots \\ b && b && b && \cdots && a \end{vmatrix}.$

where . Recall the formula for the determinant:

Now the value of the product on the right for a permutation is, where f is the number of fixed points of . Hence

$d(n) = b^n n! g\left(z, -1, \frac{a}{b}\right)= b^n n! \exp \left(\frac{a-b}{b} z\right) (1+z)$

which yields

$b^n \left(\frac{a-b}{b}\right)^n + b^n n \left(\frac{a-b}{b}\right)^{n-1} = (a-b)^n + n b (a-b)^{n-1}$

and finally

Read more about this topic: Random Permutation Statistics

Famous quotes containing the words problem, putnam and/or competition:

“The family environment in which your children are growing up is different from that in which you grew up. The decisions our parents made and the strategies they used were developed in a different context from what we face today, even if the “content” of the problem is the same. It is a mistake to think that our own experience as children and adolescents will give us all we need to help our children. The rules of the game have changed.”
—Lawrence Kutner (20th century)

“Men, you are all marksmen—don’t one of you fire until you see the whites of their eyes.”
—Israel Putnam (1718–1790)

“Like many businessmen of genius he learned that free competition was wasteful, monopoly efficient. And so he simply set about achieving that efficient monopoly.”
—Mario Puzo (b. 1920)