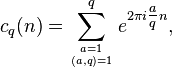Ramanujan's Sum

In number theory, a branch of mathematics, Ramanujan's sum, usually denoted cq(n), is a function of two positive integer variables q and n defined by the formula

c_q(n)= \sum_{a=1\atop (a,q)=1}^q e^{2 \pi i \tfrac{a}{q} n} ,

where (a, q) = 1 means that a only takes on values coprime to q.

Srinivasa Ramanujan introduced the sums in a 1918 paper. In addition to the expansions discussed in this article, Ramanujan's sums are used in the proof of Vinogradov's theorem that every sufficiently-large odd number is the sum of three primes.

Read more about Ramanujan's Sum:  Notation, Table, Ramanujan Expansions, See Also

Famous quotes containing the word sum:

    “The sum and substance of female education in America, as in England, is training women to consider marriage as the sole object in life, and to pretend that they do not think so.”
    —Harriet Martineau (1802–1876)