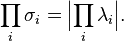Connection To A Determinant or A Product of Eigenvalues
We can use QR decomposition to find the absolute value of the determinant of a square matrix. Suppose a matrix is decomposed as . Then we have
Since Q is unitary, . Thus,
where are the entries on the diagonal of R.
Furthermore, because the determinant equals the product of the eigenvalues, we have
where are eigenvalues of .
We can extend the above properties to non-square complex matrix by introducing the definition of QR-decomposition for non-square complex matrix and replacing eigenvalues with singular values.
Suppose a QR decomposition for a non-square matrix A:
where is a zero matrix and is an unitary matrix.
From the properties of SVD and determinant of matrix, we have
where are singular values of .
Note that the singular values of and are identical, although the complex eigenvalues of them may be different. However, if A is square, it holds that
In conclusion, QR decomposition can be used efficiently to calculate a product of eigenvalues or singular values of matrix.
Read more about this topic: QR Decomposition
Famous quotes containing the words connection to, connection and/or product:
“It may comfort you to know that if your child reaches the age of eleven or twelve and you have a good bond or relationship, no matter how dramatic adolescence becomes, you children will probably turn out all right and want some form of connection to you in adulthood.”
—Charlotte Davis Kasl (20th century)
“One must always maintain one’s connection to the past and yet ceaselessly pull away from it. To remain in touch with the past requires a love of memory. To remain in touch with the past requires a constant imaginative effort.”
—Gaston Bachelard (1884–1962)
“...In the past, as now, [Hollywood] was a stamping ground for tastelessness, violence, and hyperbole, but once upon a time it turned out a product which sweetened the flavor of life all over the world.”
—Anita Loos (1888–1981)