Pumping Lemma For Regular Languages - Formal Statement

Formal Statement

Let L be a regular language. Then there exists an integer p ≥ 1 depending only on L such that every string w in L of length at least p (p is called the "pumping length") can be written as w = xyz (i.e., w can be divided into three substrings), satisfying the following conditions:

  1. |y| ≥ 1;
  2. |xy| ≤ p
  3. for all i ≥ 0, xyiz ∈ L

y is the substring that can be pumped (removed or repeated any number of times, and the resulting string is always in L). (1) means the loop y to be pumped must be of length at least one; (2) means the loop must occur within the first p characters. |x| must be smaller than p (conclusion of (1) and (2)), apart from that there is no restriction on x and z.

In simple words, for any regular language L, any sufficiently long word w (in L) can be split into 3 parts. i.e. w = xyz, such that all the strings xykz for k≥0 are also in L.

Below is a formal expression of the Pumping Lemma.

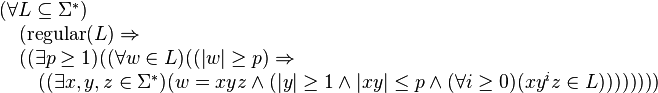
\begin{array}{l} (\forall L\subseteq \Sigma^*) \\ \quad (\mbox{regular}(L) \Rightarrow \\ \quad ((\exists p\geq 1) ( (\forall w\in L) ((|w|\geq p) \Rightarrow \\ \quad\quad ((\exists x,y,z \in \Sigma^*) (w=xyz \land (|y|\geq 1 \land |xy|\leq p \land (\forall i\geq 0)(xy^iz\in L)))))))) \end{array}

Read more about this topic:  Pumping Lemma For Regular Languages

Famous quotes containing the words formal and/or statement:

    “That anger can be expressed through words and non-destructive activities; that promises are intended to be kept; that cleanliness and good eating habits are aspects of self-esteem; that compassion is an attribute to be prized—all these lessons are ones children can learn far more readily through the living example of their parents than they ever can through formal instruction.”
    —Fred Rogers (20th century)

    “I think, therefore I am is the statement of an intellectual who underrates toothaches.”
    —Milan Kundera (b. 1929)