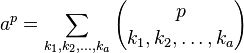Proofs of Fermat's Little Theorem - Proof Using The Multinomial Expansion

Proof Using The Multinomial Expansion

The proof is a very simple application of the Multinomial formula which is brought here for the sake of simplicity.

(x_1 + x_2 + \cdots + x_m)^n = \sum_{k_1,k_2,\ldots,k_m} {n \choose k_1, k_2, \ldots, k_m} x_1^{k_1} x_2^{k_2} \cdots x_m^{k_m}.

The summation is taken over all sequences of nonnegative integer indices k1 through km such the sum of all ki is n.

Thus if we express a as a sum of 1s (ones), we obtain

a^p = \sum_{k_1,k_2,\ldots,k_a} {p \choose k_1, k_2, \ldots, k_a}

Clearly, if p is prime, and if kj not equal to p for any j, we have

and

if kj equal to p for some j

Since there are exactly a elements such that the theorem follows.

Read more about this topic:  Proofs Of Fermat's Little Theorem

Famous quotes containing the words proof and/or expansion:

    “Sculpture and painting are very justly called liberal arts; a lively and strong imagination, together with a just observation, being absolutely necessary to excel in either; which, in my opinion, is by no means the case of music, though called a liberal art, and now in Italy placed even above the other two—a proof of the decline of that country.”
    —Philip Dormer Stanhope, 4th Earl Chesterfield (1694–1773)

    “We are caught up Mr. Perry on a great wave whether we will or no, a great wave of expansion and progress. All these mechanical inventions—telephones, electricity, steel bridges, horseless vehicles—they are all leading somewhere. It’s up to us to be on the inside in the forefront of progress.”
    —John Dos Passos (1896–1970)