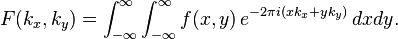Projection-slice Theorem - Proof in Two Dimensions

Proof in Two Dimensions

The projection-slice theorem is easily proven for the case of two dimensions. Without loss of generality, we can take the projection line to be the x-axis. There is no loss of generality because using a shifted and rotated line the law still applies. Using a shifted line (in y) gives the same projection and therefore the same 1D Fourier transform. Rotated function is the Fourier pair of the rotated Fourier transform, this completes the explanation.

If f(x, y) is a two-dimensional function, then the projection of f(x, y) onto the x axis is p(x) where

The Fourier transform of is

F(k_x,k_y)=\int_{-\infty}^\infty \int_{-\infty}^\infty f(x,y)\,e^{-2\pi i(xk_x+yk_y)}\,dxdy.

The slice is then

s(k_x)=F(k_x,0) =\int_{-\infty}^\infty \int_{-\infty}^\infty f(x,y)\,e^{-2\pi ixk_x}\,dxdy
=\int_{-\infty}^\infty \left\,e^{-2\pi ixk_x} dx
=\int_{-\infty}^\infty p(x)\,e^{-2\pi ixk_x} dx

which is just the Fourier transform of p(x). The proof for higher dimensions is easily generalized from the above example.

Read more about this topic:  Projection-slice Theorem

Famous quotes containing the words proof and/or dimensions:

    “From whichever angle one looks at it, the application of racial theories remains a striking proof of the lowered demands of public opinion upon the purity of critical judgment.”
    —Johan Huizinga (1872–1945)

    “Is it true or false that Belfast is north of London? That the galaxy is the shape of a fried egg? That Beethoven was a drunkard? That Wellington won the battle of Waterloo? There are various degrees and dimensions of success in making statements: the statements fit the facts always more or less loosely, in different ways on different occasions for different intents and purposes.”
    —J.L. (John Langshaw)