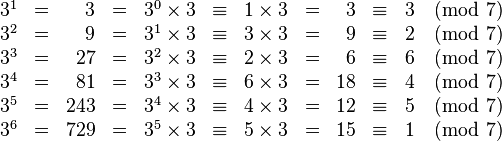Primitive Root Modulo n - Elementary Example

Elementary Example

The number 3 is a primitive root modulo 7 because

\begin{array}{rcrcrcrcrcr} 3^1 &=& 3 &=& 3^0 \times 3 &\equiv& 1 \times 3 &=& 3 &\equiv& 3 \pmod 7 \\ 3^2 &=& 9 &=& 3^1 \times 3 &\equiv& 3 \times 3 &=& 9 &\equiv& 2 \pmod 7 \\ 3^3 &=& 27 &=& 3^2 \times 3 &\equiv& 2 \times 3 &=& 6 &\equiv& 6 \pmod 7 \\ 3^4 &=& 81 &=& 3^3 \times 3 &\equiv& 6 \times 3 &=& 18 &\equiv& 4 \pmod 7 \\ 3^5 &=& 243 &=& 3^4 \times 3 &\equiv& 4 \times 3 &=& 12 &\equiv& 5 \pmod 7 \\ 3^6 &=& 729 &=& 3^5 \times 3 &\equiv& 5 \times 3 &=& 15 &\equiv& 1 \pmod 7 \\ \end{array}

Here we see that the period of 3k modulo 7 is 6. The remainders in the period, which are 3, 2, 6, 4, 5, 1, form a rearrangement of all nonzero remainders modulo 7, implying that 3 is indeed a primitive root modulo 7. Curiously, permutations created in this way (and their circular shifts) have been shown to be Costas arrays.

Read more about this topic:  Primitive Root Modulo n

Famous quotes containing the word elementary:

    “As if paralyzed by the national fear of ideas, the democratic distrust of whatever strikes beneath the prevailing platitudes, it evades all resolute and honest dealing with what, after all, must be every healthy literature’s elementary materials.”
    —H.L. (Henry Lewis)

    “If men as individuals surrender to the call of their elementary instincts, avoiding pain and seeking satisfaction only for their own selves, the result for them all taken together must be a state of insecurity, of fear, and of promiscuous misery.”
    —Albert Einstein (1879–1955)