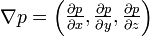Pressure Gradient - Mathematical Description

Mathematical Description

Assuming that the pressure p is an intensive quantity, i.e., a single-valued, continuous and differentiable function of three-dimensional space (often called a scalar field), i.e., that

where x, y and z are the coordinates of the location of interest, then the pressure gradient is the vector quantity defined as

\nabla p = \begin{pmatrix} {\frac{\partial p}{\partial x}}, {\frac{\partial p}{\partial y}}, {\frac{\partial p}{\partial z}} \end{pmatrix}

Read more about this topic:  Pressure Gradient

Famous quotes containing the words mathematical and/or description:

    “What he loved so much in the plant morphological structure of the tree was that given a fixed mathematical basis, the final evolution was so incalculable.”
    —D.H. (David Herbert)

    “Why does philosophy use concepts and why does faith use symbols if both try to express the same ultimate? The answer, of course, is that the relation to the ultimate is not the same in each case. The philosophical relation is in principle a detached description of the basic structure in which the ultimate manifests itself. The relation of faith is in principle an involved expression of concern about the meaning of the ultimate for the faithful.”
    —Paul Tillich (1886–1965)