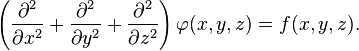Poisson's Equation - Statement of The Equation

Statement of The Equation

The Poisson Equation is

where is the Laplace operator, and f and φ are real or complex-valued functions on a manifold. When the manifold is Euclidean space, the Laplace operator is often denoted as ∇2 and so Poisson's equation is frequently written as

In three-dimensional Cartesian coordinates, it takes the form

\left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \right)\varphi(x,y,z) = f(x,y,z).

For vanishing f, this equation becomes Laplace's equation

The Poisson equation may be solved using a Green's function; a general exposition of the Green's function for the Poisson equation is given in the article on the screened Poisson equation. There are various methods for numerical solution. The relaxation method, an iterative algorithm, is one example.

Read more about this topic:  Poisson's Equation

Famous quotes containing the words statement of the, statement of, statement and/or equation:

    “It is commonplace that a problem stated is well on its way to solution, for statement of the nature of a problem signifies that the underlying quality is being transformed into determinate distinctions of terms and relations or has become an object of articulate thought.”
    —John Dewey (1859–1952)

    “Eloquence must be grounded on the plainest narrative. Afterwards, it may warm itself until it exhales symbols of every kind and color, speaks only through the most poetic forms; but first and last, it must still be at bottom a biblical statement of fact.”
    —Ralph Waldo Emerson (1803–1882)

    “The force of truth that a statement imparts, then, its prominence among the hordes of recorded observations that I may optionally apply to my own life, depends, in addition to the sense that it is argumentatively defensible, on the sense that someone like me, and someone I like, whose voice is audible and who is at least notionally in the same room with me, does or can possibly hold it to be compellingly true.”
    —Nicholson Baker (b. 1957)

    “A nation fights well in proportion to the amount of men and materials it has. And the other equation is that the individual soldier in that army is a more effective soldier the poorer his standard of living has been in the past.”
    —Norman Mailer (b. 1923)