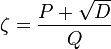Relation To Quadratic Irrationals
A quadratic irrational number is an irrational real root of the quadratic equation
where the coefficients a, b, and c are integers, and the discriminant, b2 − 4ac, is greater than zero. By the quadratic formula every quadratic irrational can be written in the form
where P, D, and Q are integers, D > 0 is not a perfect square, and Q divides the quantity P2 − D.
By considering the complete quotients of periodic continued fractions, Euler was able to prove that if x is a regular periodic continued fraction, then x is a quadratic irrational number. The proof is straightforward. From the fraction itself, one can construct the quadratic equation with integral coefficients that x must satisfy.
Lagrange proved the converse of Euler's theorem: if x is a quadratic irrational, then the regular continued fraction expansion of x is periodic. Given a quadratic irrational x one can construct m different quadratic equations, each with the same discriminant, that relate the successive complete quotients of the regular continued fraction expansion of x to one another. Since there are only finitely many of these equations (the coefficients are bounded), the complete quotients (and also the partial denominators) in the regular continued fraction that represents x must eventually repeat.
Read more about this topic: Periodic Continued Fraction
Famous quotes containing the words relation to and/or relation:
“The psychoanalysis of individual human beings, however, teaches us with quite special insistence that the god of each of them is formed in the likeness of his father, that his personal relation to God depends on his relation to his father in the flesh and oscillates and changes along with that relation, and that at bottom God is nothing other than an exalted father.”
—Sigmund Freud (1856–1939)
“Skepticism is unbelief in cause and effect. A man does not see, that, as he eats, so he thinks: as he deals, so he is, and so he appears; he does not see that his son is the son of his thoughts and of his actions; that fortunes are not exceptions but fruits; that relation and connection are not somewhere and sometimes, but everywhere and always; no miscellany, no exemption, no anomaly,—but method, and an even web; and what comes out, that was put in.”
—Ralph Waldo Emerson (1803–1882)