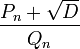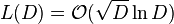Periodic Continued Fraction - Length of The Repeating Block

Length of The Repeating Block

By analyzing the sequence of combinations

\frac{P_n + \sqrt{D}}{Q_n}

that can possibly arise when ζ = (P + √D)/Q is expanded as a regular continued fraction, Lagrange showed that the largest partial denominator ai in the expansion is less than 2√D, and that the length of the repeating block is less than 2D.

More recently, sharper arguments based on the divisor function have shown that L(D), the length of the repeating block for a quadratic surd of discriminant D, is given by

L(D) = \mathcal{O}(\sqrt{D}\ln{D})

where the big O means "on the order of", or "asymptotically proportional to" (see big O notation).

Read more about this topic:  Periodic Continued Fraction

Famous quotes containing the words length, repeating and/or block:

    “At length to hospital
    This man was limited,
    Where screens leant on the wall
    And idle headphones hung.
    Since he would soon be dead
    They let his wife come along
    And pour out tea, each day.”
    —Philip Larkin (1922–1986)

    “If these were only words that I am speaking
    Indifferent sounds and not the heraldic-ho
    Of the clear sovereign that is reality,
    Of the clearest reality that is sovereign,
    How should I repeat them, keep repeating them....”
    —Wallace Stevens (1879–1955)

    “Painting consumes labour not disproportionate to its effect; but a fellow will hack half a year at a block of marble to make something in stone that hardly resembles a man. The value of statuary is owing to its difficulty. You would not value the finest head cut upon a carrot.”
    —Samuel Johnson (1709–1784)