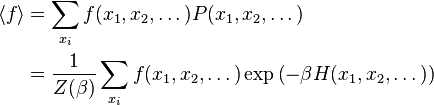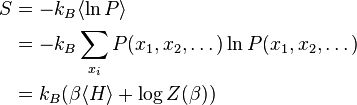Partition Function (mathematics) - Expectation Values

Expectation Values

The partition function is commonly used as a generating function for expectation values of various functions of the random variables. So, for example, taking as an adjustable parameter, then the derivative of with respect to

gives the average (expectation value) of H. In physics, this would be called the average energy of the system.

Given the definition of the probability measure above, the expectation value of any function f of the random variables X may now be written as expected: so, for discrete-valued X, one writes

\begin{align} \langle f\rangle & = \sum_{x_i} f(x_1,x_2,\dots) P(x_1,x_2,\dots) \\ & = \frac{1}{Z(\beta)} \sum_{x_i} f(x_1,x_2,\dots) \exp \left(-\beta H(x_1,x_2,\dots) \right) \end{align}

The above notation is strictly correct for a finite number of discrete random variables, but should be seen to be somewhat 'informal' for continuous variables; properly, the summations above should be replaced with the notations of the underlying sigma algebra used to define a probability space. That said, the identities continue to hold, when properly formulated on a measure space.

Thus, for example, the entropy is given by

\begin{align} S & = -k_B \langle\ln P\rangle \\ & = -k_B\sum_{x_i} P(x_1,x_2,\dots) \ln P(x_1,x_2,\dots) \\ & = k_B(\beta \langle H\rangle + \log Z(\beta)) \end{align}

The Gibbs measure is the unique statistical distribution that maximizes the entropy for a fixed expectation value of the energy; this underlies its use in maximum entropy methods.

Read more about this topic:  Partition Function (mathematics)

Famous quotes containing the words expectation and/or values:

    “Often, when there is a conflict between parent and child, at its very hub is an expectation that the child should be acting differently. Sometimes these expectations run counter what is known about children’s growth. They stem from remembering oneself, but usually at a slightly older age.”
    —Ellen Galinsky (20th century)

    “Tallulah [Bankhead] was the foremost naughty girl of her era but, in those days, “naughty” meant piquant, whereas values have so changed that now, in the 1970s, it generally means nauseating.”
    —Anita Loos (1888–1981)