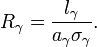Partial Element Equivalent Circuit - Theory

Theory

The classical PEEC method is derived from the equation for the total electric field at a point written as

\vec{E}^i(\vec{r},t) = \frac{\vec{J}(\vec{r},t)}{\sigma} + \frac {\partial \vec{A}(\vec{r},t)}{\partial t} + \nabla \phi (\vec{r},t)

where is an incident electric field, is a current density, is the magnetic vector potential, is the scalar electric potential, and the electrical conductivity all at observation point . In the figures on the right, an orthogonal metal strip with 3 nodes and 2 cells, and the corresponding PEEC circuit are shown.

By using the definitions of the scalar and vector potentials, the current- and charge-densities are discretized by defining pulse basis functions for the conductors and dielectric materials. Pulse functions are also used for the weighting functions resulting in a Galerkin type solution. By defining a suitable inner product, a weighted volume integral over the cells, the field equation can be interpreted as Kirchhoff's voltage law over a PEEC cell consisting of partial self inductances between the nodes and partial mutual inductances representing the magnetic field coupling in the equivalent circuit. The partial inductances are defined as

L_{p_{\alpha \beta}} = \frac {\mu}{4 \pi}\frac{1}{a_{\alpha} a_{\beta}} \int_{v_{\alpha}} \int_{v_{\beta}} \frac {1} {| \vec{r}_{\alpha} - \vec{r}_{\beta}|} d v_{\alpha} dv_{\beta}

for volume cell and . Then, the coefficients of potentials are computed as

P_{ij} = \frac{1}{S_i S_j} \frac{1}{4 \pi \epsilon_0} \int_{S_i} \int_{S_j} \frac{1}{|\vec{r}_i - \vec{r}_j|} \; dS_j \; dS_i

and a resistive term between the nodes, defined as

R_\gamma = \frac{l_\gamma}{a_\gamma \sigma_\gamma}.

Read more about this topic:  Partial Element Equivalent Circuit

Famous quotes containing the word theory:

    “By the “mud-sill” theory it is assumed that labor and education are incompatible; and any practical combination of them impossible. According to that theory, a blind horse upon a tread-mill, is a perfect illustration of what a laborer should be—all the better for being blind, that he could not tread out of place, or kick understandingly.... Free labor insists on universal education.”
    —Abraham Lincoln (1809–1865)

    “The struggle for existence holds as much in the intellectual as in the physical world. A theory is a species of thinking, and its right to exist is coextensive with its power of resisting extinction by its rivals.”
    —Thomas Henry Huxley (1825–95)

    “Freud was a hero. He descended to the “Underworld” and met there stark terrors. He carried with him his theory as a Medusa’s head which turned these terrors to stone.”
    —R.D. (Ronald David)