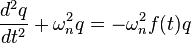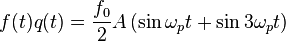Parametric Oscillator - Intuitive Derivation of Parametric Excitation

Intuitive Derivation of Parametric Excitation

The above derivation may seem like a mathematical sleight-of-hand, so it may be helpful to give an intuitive derivation. The equation may be written in the form

which represents a simple harmonic oscillator (or, alternatively, a bandpass filter) being driven by a signal that is proportional to its response .

Assume that already has an oscillation at frequency and that the pumping has double the frequency and a small amplitude . Applying a trigonometric identity for products of sinusoids, their product produces two driving signals, one at frequency and the other at frequency

Being off-resonance, the signal is attentuated and can be neglected initially. By contrast, the signal is on resonance, serves to amplify and is proportional to the amplitude . Hence, the amplitude of grows exponentially unless it is initially zero.

Expressed in Fourier space, the multiplication is a convolution of their Fourier transforms and . The positive feedback arises because the component of converts the component of into a driving signal at, and vice versa (reverse the signs). This explains why the pumping frequency must be near, twice the natural frequency of the oscillator. Pumping at a grossly different frequency would not couple (i.e., provide mutual positive feedback) between the and components of .