Parabolic Trajectory - Barker's Equation

Barker's Equation

Barker's equation relates the time of flight to the true anomaly of a parabolic trajectory.

t - T = \frac{1}{2}\sqrt{\frac{p^{3}}{\mu}}\left (D + \frac{1}{3}D^{3}\right )

Where:

  • D = tan(ν/2), ν is the true anomaly of the orbit
  • t is the current time in seconds
  • T is the time of periapsis passage in seconds
  • μ is the standard gravitational parameter
  • p is the semi-latus rectum of the trajectory ( p = h2/μ )

More generally, the time between any two points on an orbit is

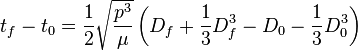
t_{f} - t_{0} = \frac{1}{2}\sqrt{\frac{p^{3}}{\mu}}\left (D_{f} + \frac{1}{3}D_{f}^{3} - D_{0} - \frac{1}{3}D_{0}^{3}\right )


Alternately, the equation can be expressed in terms of periapsis distance, in a parabolic orbit rp = p/2:

t - T = \sqrt{\frac{2r_{p}^{3}}{\mu}}\left (D + \frac{1}{3}D^{3}\right )

Unlike Kepler's equation, which is used to solve for true anomalies in elliptical and hyperbolic trajectories, the true anomaly in Barker's equation can be solved directly for t. If the following substitutions are made

A = \frac{3}{2}\sqrt{\frac{\mu}{2r_{p}^{3}}}(t-T)

B = \sqrt{A + \sqrt{A^{2}+1}}

then

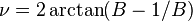
\nu = 2\arctan(B - 1/B)

Read more about this topic:  Parabolic Trajectory

Famous quotes containing the words barker and/or equation:

    “The love that kisses with a homicide
    In robes of red generation resurrects.”
    —George Barker (b. 1913)

    “Jail sentences have many functions, but one is surely to send a message about what our society abhors and what it values. This week, the equation was twofold: female infidelity twice as bad as male abuse, the life of a woman half as valuable as that of a man. The killing of the woman taken in adultery has a long history and survives today in many cultures. One of those is our own.”
    —Anna Quindlen (b. 1952)