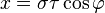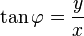Parabolic Coordinates - Three-dimensional Parabolic Coordinates

Three-dimensional Parabolic Coordinates

The two-dimensional parabolic coordinates form the basis for two sets of three-dimensional orthogonal coordinates. The parabolic cylindrical coordinates are produced by projecting in the -direction. Rotation about the symmetry axis of the parabolae produces a set of confocal paraboloids, forming a coordinate system that is also known as "parabolic coordinates"

x = \sigma \tau \cos \varphi
y = \sigma \tau \sin \varphi
z = \frac{1}{2} \left(\tau^{2} - \sigma^{2} \right)

where the parabolae are now aligned with the -axis, about which the rotation was carried out. Hence, the azimuthal angle is defined

\tan \varphi = \frac{y}{x}

The surfaces of constant form confocal paraboloids

2z = \frac{x^{2} + y^{2}}{\sigma^{2}} - \sigma^{2}

that open upwards (i.e., towards ) whereas the surfaces of constant form confocal paraboloids

2z = -\frac{x^{2} + y^{2}}{\tau^{2}} + \tau^{2}

that open downwards (i.e., towards ). The foci of all these paraboloids are located at the origin.

The Riemannian metric tensor associated with this coordinate system is

Read more about this topic:  Parabolic Coordinates