Properties in Finite-dimensional Case
If a normal operator on a finite-dimensional real or complex Hilbert space (inner product space) stabilizes a subspace, then it also stabilizes its orthogonal complement . (This statement is trivial in the case where is self-adjoint )
Proof. Denote by the orthogonal projection onto . Then the orthogonal projection onto is . The fact that stabilizes can be expressed as, or . The goal is to show that . Since is an inner product on the space of endomorphisms of, it is enough to show that . This follows from a direct computation, using properties of the trace and of orthogonal projections:
,
.
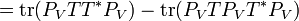
The same argument goes through for compact normal operators in infinite dimensional Hilbert spaces, where one make use of the Hilbert-Schmidt inner product. However, for bounded normal operators orthogonal complement to a stable subspace may not be stable. It follows that such subspaces cannot be spanned by eigenvectors. Consider, for example, the bilateral shift, which has no eigenvalues. The invariant subspaces of the bilateral shift is characterized by Beurling's theorem.
Read more about this topic: Normal Operator
Famous quotes containing the words properties and/or case:
“A drop of water has the properties of the sea, but cannot exhibit a storm. There is beauty of a concert, as well as of a flute; strength of a host, as well as of a hero.”
—Ralph Waldo Emerson (1803–1882)
“Sculpture and painting are very justly called liberal arts; a lively and strong imagination, together with a just observation, being absolutely necessary to excel in either; which, in my opinion, is by no means the case of music, though called a liberal art, and now in Italy placed even above the other two—a proof of the decline of that country.”
—Philip Dormer Stanhope, 4th Earl Chesterfield (1694–1773)