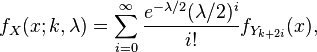Noncentral Chi-squared Distribution - Definition

Definition

The probability density function is given by

f_X(x; k,\lambda) = \sum_{i=0}^\infty \frac{e^{-\lambda/2} (\lambda/2)^i}{i!} f_{Y_{k+2i}}(x),

where is distributed as chi-squared with degrees of freedom.

From this representation, the noncentral chi-squared distribution is seen to be a Poisson-weighted mixture of central chi-squared distributions. Suppose that a random variable J has a Poisson distribution with mean, and the conditional distribution of Z given is chi-squared with k+2i degrees of freedom. Then the unconditional distribution of Z is non-central chi-squared with k degrees of freedom, and non-centrality parameter .

Alternatively, the pdf can be written as

where is a modified Bessel function of the first kind given by

Using the relation between Bessel functions and hypergeometric functions, the pdf can also be written as:

Siegel (1979) discusses the case k=0 specifically (zero degrees of freedom), in which case the distribution has a discrete component at zero.

Read more about this topic:  Noncentral Chi-squared Distribution

Famous quotes containing the word definition:

    “It’s a rare parent who can see his or her child clearly and objectively. At a school board meeting I attended . . . the only definition of a gifted child on which everyone in the audience could agree was “mine.””
    —Jane Adams (20th century)

    “The physicians say, they are not materialists; but they are:MSpirit is matter reduced to an extreme thinness: O so thin!—But the definition of spiritual should be, that which is its own evidence. What notions do they attach to love! what to religion! One would not willingly pronounce these words in their hearing, and give them the occasion to profane them.”
    —Ralph Waldo Emerson (1803–1882)

    “I’m beginning to think that the proper definition of “Man” is “an animal that writes letters.””
    —Lewis Carroll [Charles Lutwidge Dodgson] (1832–1898)