n-body Problem - The Global Solution of The n-body Problem

The Global Solution of The n-body Problem

In order to generalize Sundman's result for the case n > 3 (or n = 3 and c = 0) one has to face two obstacles:

  1. As it has been shown by Siegel, collisions which involve more than 2 bodies cannot be regularized analytically, hence Sundman's regularization cannot be generalized.
  2. The structure of singularities is more complicated in this case: other types of singularities may occur.

Finally Sundman's result was generalized to the case of n > 3 bodies by Q. Wang in the 1990s. Since the structure of singularities is more complicated, Wang had to leave out completely the questions of singularities. The central point of his approach is to transform, in an appropriate manner, the equations to a new system, such that the interval of existence for the solutions of this new system is 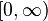[0,\infty) .

Read more about this topic:  n-body Problem

Famous quotes containing the words global, solution and/or problem:

    “As the global expansion of Indian and Chinese restaurants suggests, xenophobia is directed against foreign people, not foreign cultural imports.”
    —Eric J. Hobsbawm (b. 1917)

    “Let us begin to understand the argument.
    There is a solution to everything: Science.”
    —Allen Tate (1899–1979)

    “The family environment in which your children are growing up is different from that in which you grew up. The decisions our parents made and the strategies they used were developed in a different context from what we face today, even if the “content” of the problem is the same. It is a mistake to think that our own experience as children and adolescents will give us all we need to help our children. The rules of the game have changed.”
    —Lawrence Kutner (20th century)