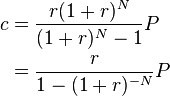Mortgage Calculator - Monthly Payment Formula

Monthly Payment Formula

The fixed monthly payment for a fixed rate mortgage is the amount paid by the borrower every month that ensures that the loan is paid off in full with interest at the end of its term. The monthly payment formula is based on the annuity formula. The monthly payment c depends upon:

• r - the monthly interest rate, expressed as a decimal, not a percentage. Since the quoted yearly percentage rate is not a compounded rate, the monthly percentage rate is simply the yearly percentage rate divided by 12; dividing the monthly percentage rate by 100 gives r, the monthly rate expressed as a decimal.
• N - the number of monthly payments, called the loan's term, and
• P - the amount borrowed, known as the loan's principal.

In the standardized calculations used in the United States, c is given by the formula:

For example, for a home loan for $200,000 with a fixed yearly interest rate of 6.5% for 30 years, the principal is, the monthly interest rate is, the number of monthly payments is, the fixed monthly payment equals $1264.14. This formula is provided using the financial function PMT in a spreadsheet such as Excel. In the example, the monthly payment is obtained by entering either of the these formulas:

=PMT(6.5/100/12,30*12,200000)

=((6.5/100/12) * 200000) / (1 - ((1 + (6.5/100/12)) ^ (-30*12)))

The following derivation of this formula illustrates how fixed-rate mortgage loans work. The amount owed on the loan at the end of every month equals the amount owed from the previous month, plus the interest on this amount, minus the fixed amount paid every month. This fact results in the debt schedule:

Amount owed at initiation:

Amount owed after 1 month:

Amount owed after 2 months:

Amount owed after 3 months:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Amount owed after N months:

The polynomial appearing before the fixed monthly payment c (with ) is called a cyclotomic polynomial; it has a simple closed-form expression obtained from observing that because all but the first and last terms in this difference cancel each other out. Therefore, solving for yields the much simpler closed-form expression

Applying this fact about cyclotomic polynomials to the amount owed at the end of the Nth month gives (using to succinctly denote the function value at argument value x = (1+r )):

Amount owed at end of month N

The amount of the monthly payment at the end of month N that is applied to principal paydown equals the amount c of payment minus the amount of interest currently paid on the pre-existing unpaid principal. The latter amount, the interest component of the current payment, is the interest rate r times the amount unpaid at the end of month N–1. Since in the early years of the mortgage the unpaid principal is still large, so are the interest payments on it; so the portion of the monthly payment going toward paying down the principal is very small and equity in the property accumulates very slowly (in the absence of changes in the market value of the property). But in the later years of the mortgage, when the principal has already been substantially paid down and not much monthly interest needs to be paid, most of the monthly payment goes toward repayment of the principal, and the remaining principal declines rapidly.

The borrower's equity in the property equals the current market value of the property minus the amount owed according to the above formula.

With a fixed rate mortgage, the borrower agrees to pay off the loan completely at the end of the loan's term, so the amount owed at month N must be zero. For this to happen, the monthly payment c can be obtained from the previous equation to obtain:

which is the formula originally provided. This derivation illustrates three key components of fixed-rate loans: (1) the fixed monthly payment depends upon the amount borrowed, the interest rate, and the length of time over which the loan is repaid; (2) the amount owed every month equals the amount owed from the previous month plus interest on that amount, minus the fixed monthly payment; (3) the fixed monthly payment is chosen so that the loan is paid off in full with interest at the end of its term and no more money is owed.