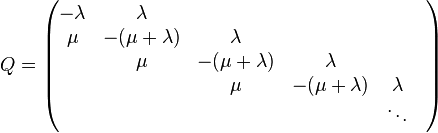M/M/1 Queue - Model Definition

Model Definition

An M/M/1 queue is a stochastic process whose state space is the set {0,1,2,3,...} where the value corresponds to the number of customers in the system, including any currently in service.

Arrivals occur at rate λ according to a Poisson process and move the process from state i to i + 1.
Service times have an exponential distribution with parameter μ in the M/M/1 queue.
A single server serves customers one at a time from the front of the queue, according to a first-come, first-served discipline. When the service is complete the customer leaves the queue and the number of customers in the system reduces by one.
The buffer is of infinite size, so there is no limit on the number of customers it can contain.

The model can be described as a continuous time Markov chain with transition rate matrix

$Q=\begin{pmatrix} -\lambda & \lambda \\ \mu & -(\mu+\lambda) & \lambda \\ &\mu & -(\mu+\lambda) & \lambda \\ &&\mu & -(\mu+\lambda) & \lambda &\\ &&&&\ddots \end{pmatrix}$

on the state space {0,1,2,3,...}. This is the same continuous time Markov chain as in a birth–death process. The state space diagram for this chain is as below.

Famous quotes containing the words model and/or definition:

“If the man who paints only the tree, or flower, or other surface he sees before him were an artist, the king of artists would be the photographer. It is for the artist to do something beyond this: in portrait painting to put on canvas something more than the face the model wears for that one day; to paint the man, in short, as well as his features.”
—James Mcneill Whistler (1834–1903)

“The man who knows governments most completely is he who troubles himself least about a definition which shall give their essence. Enjoying an intimate acquaintance with all their particularities in turn, he would naturally regard an abstract conception in which these were unified as a thing more misleading than enlightening.”
—William James (1842–1910)