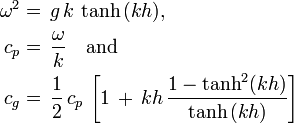Mild-slope Equation - Formulation For Monochromatic Wave Motion

Formulation For Monochromatic Wave Motion

For monochromatic waves according to linear theory—with the free surface elevation given as and the waves propagating on a fluid layer of mean water depth —the mild-slope equation is:

where:

  • is the complex-valued amplitude of the free-surface elevation
  • is the horizontal position;
  • is the angular frequency of the monochromatic wave motion;
  • is the imaginary unit;
  • means taking the real part of the quantity between braces;
  • is the horizontal gradient operator;
  • is the divergence operator;
  • is the wavenumber;
  • is the phase speed of the waves and
  • is the group speed of the waves.

The phase and group speed depend on the dispersion relation, and are derived from Airy wave theory as:

\begin{align} \omega^2 &=\, g\, k\, \tanh\, (kh), \\ c_p &=\, \frac{\omega}{k} \quad \text{and} \\ c_g &=\, \frac12\, c_p\, \left \end{align}

where

  • is Earth's gravity and
  • is the hyperbolic tangent.

For a given angular frequency, the wavenumber has to be solved from the dispersion equation, which relates these two quantities to the water depth .

Read more about this topic:  Mild-slope Equation

Famous quotes containing the words formulation, wave and/or motion:

    “You do not mean by mystery what a Catholic does. You mean an interesting uncertainty: the uncertainty ceasing interest ceases also.... But a Catholic by mystery means an incomprehensible certainty: without certainty, without formulation there is no interest;... the clearer the formulation the greater the interest.”
    —Gerard Manley Hopkins (1844–1889)

    “We are caught up Mr. Perry on a great wave whether we will or no, a great wave of expansion and progress. All these mechanical inventions—telephones, electricity, steel bridges, horseless vehicles—they are all leading somewhere. It’s up to us to be on the inside in the forefront of progress.”
    —John Dos Passos (1896–1970)

    “Motion or change, and identity or rest, are the first and second secrets of nature: Motion and Rest. The whole code of her laws may be written on the thumbnail, or the signet of a ring.”
    —Ralph Waldo Emerson (1803–1882)