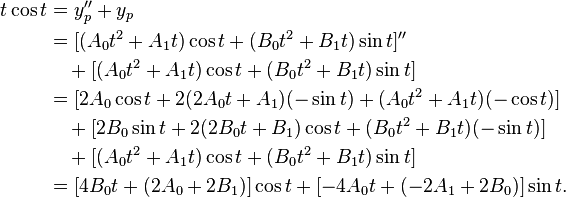Method of Undetermined Coefficients - Examples

Examples

Example 1

Find a particular integral of the equation

The right side t cos t has the form

with n=1, α=0, and β=1.

Since α + iβ = i is a simple root of the characteristic equation

we should try a particular integral of the form

\begin{align} y_p &= t \\ &= t \\ &= t \\ &= (A_0 t^2 + A_1 t) \cos{t} + (B_0 t^2 + B_1 t) \sin{t} .\\ \end{align}

Substituting yp into the differential equation, we have the identity

\begin{align}t \cos{t} &= y_p'' + y_p \\ &= '' \\ &\quad + \\ &= \\ &\quad + \\ &\quad + \\ &= \cos{t} + \sin{t}. \\ \end{align}

Comparing both sides, we have

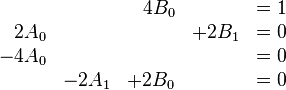
\begin{array}{rrrrl} &&4B_0&&=1\\ 2A_0 &&& + 2B_1 &= 0 \\ -4A_0 &&&& = 0 \\ &-2A_1 &+ 2B_0 && = 0 \\ \end{array}

which has the solution = 0, = 1/4, = 1/4, = 0. We then have a particular integral

Example 2

Consider the following linear nonhomogeneous differential equation:

This is like the first example above, except that the nonhomogeneous part is not linearly independent to the general solution of the homogeneous part ; as a result, we have to multiply our guess by a sufficiently large power of x to make it linearly independent.

Here our guess becomes:

By substituting this function and its derivative into the differential equation, one can solve for A:

So, the general solution to this differential equation is thus:

Example 3

Find the general solution of the equation:

f(t), is a polynomial of degree 2, so we look for a solution using the same form,

, where

Plugging this particular integral with constants A, B, and C into the original equation yields,

, where
and and

Replacing resulting constants,

To solve for the general solution,

where is the homogeneous solution, therefore, the general solution is:

Read more about this topic:  Method Of Undetermined Coefficients

Famous quotes containing the word examples:

    “In the examples that I here bring in of what I have [read], heard, done or said, I have refrained from daring to alter even the smallest and most indifferent circumstances. My conscience falsifies not an iota; for my knowledge I cannot answer.”
    —Michel de Montaigne (1533–1592)

    “There are many examples of women that have excelled in learning, and even in war, but this is no reason we should bring ‘em all up to Latin and Greek or else military discipline, instead of needle-work and housewifry.”
    —Bernard Mandeville (1670–1733)

    “Histories are more full of examples of the fidelity of dogs than of friends.”
    —Alexander Pope (1688–1744)