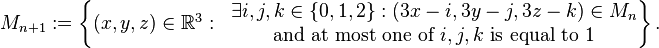Menger Sponge - Formal Definition

Famous quotes containing the words formal and/or definition:

“It is in the nature of allegory, as opposed to symbolism, to beg the question of absolute reality. The allegorist avails himself of a formal correspondence between “ideas” and “things,” both of which he assumes as given; he need not inquire whether either sphere is “real” or whether, in the final analysis, reality consists in their interaction.”
—Charles, Jr. Feidelson, U.S. educator, critic. Symbolism and American Literature, ch. 1, University of Chicago Press (1953)

“Mothers often are too easily intimidated by their children’s negative reactions...When the child cries or is unhappy, the mother reads this as meaning that she is a failure. This is why it is so important for a mother to know...that the process of growing up involves by definition things that her child is not going to like. Her job is not to create a bed of roses, but to help him learn how to pick his way through the thorns.”
—Elaine Heffner (20th century)