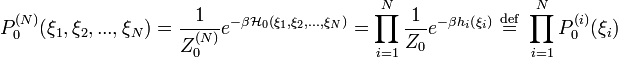Mean Field Theory - Formal Approach

Formal Approach

The formal basis for mean field theory is the Bogoliubov inequality. This inequality states that the free energy of a system with Hamiltonian

has the following upper bound:

where is the entropy and where the average is taken over the equilibrium ensemble of the reference system with Hamiltonian . In the special case that the reference Hamiltonian is that of a non-interacting system and can thus be written as

where is shorthand for the degrees of freedom of the individual components of our statistical system (atoms, spins and so forth). One can consider sharpening the upper bound by minimizing the right hand side of the inequality. The minimizing reference system is then the "best" approximation to the true system using non-correlated degrees of freedom, and is known as the mean field approximation.

For the most common case that the target Hamiltonian contains only pairwise interactions, i.e.,

where is the set of pairs that interact, the minimizing procedure can be carried out formally. Define as the generalized sum of the observable over the degrees of freedom of the single component (sum for discrete variables, integrals for continuous ones). The approximating free energy is given by

where is the probability to find the reference system in the state specified by the variables . This probability is given by the normalized Boltzmann factor

P^{(N)}_{0}(\xi_{1},\xi_{2},...,\xi_{N})=\frac{1}{Z^{(N)}_{0}}e^{-\beta \mathcal{H}_{0}(\xi_{1},\xi_{2},...,\xi_{N})}=\prod_{i=1}^{N}\frac{1}{Z_{0}}e^{-\beta h_{i}\left( \xi_{i}\right)} \ \stackrel{\mathrm{def}}{=}\ \prod_{i=1}^{N} P^{(i)}_{0}(\xi_{i})

where is the partition function. Thus

F_{0}=\sum_{(i,j)\in\mathcal{P}} {\rm Tr}_{i,j}V_{i,j}\left( \xi_{i},\xi_{j}\right)P^{(i)}_{0}(\xi_{i})P^{(j)}_{0}(\xi_{j})+ kT \sum_{i=1}^{N} {\rm Tr}_{i} P^{(i)}_{0}(\xi_{i}) \log P^{(i)}_{0}(\xi_{i}).

In order to minimize we take the derivative with respect to the single degree-of-freedom probabilities using a Lagrange multiplier to ensure proper normalization. The end result is the set of self-consistency equations

where the mean field is given by

Read more about this topic:  Mean Field Theory

Famous quotes containing the words formal and/or approach:

    “True variety is in that plenitude of real and unexpected elements, in the branch charged with blue flowers thrusting itself, against all expectations, from the springtime hedge which seems already too full, while the purely formal imitation of variety ... is but void and uniformity, that is, that which is most opposed to variety....”
    —Marcel Proust (1871–1922)

    “A lady with whom I was riding in the forest said to me that the woods always seemed to her to wait, as if the genii who inhabit them suspend their deeds until the wayfarer had passed onward; a thought which poetry has celebrated in the dance of the fairies, which breaks off on the approach of human feet.”
    —Ralph Waldo Emerson (1803–1882)