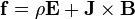Maxwell Stress Tensor - Motivation

Motivation

As outlined below, the electromagnetic force is written in terms of E and B, using vector calculus and Maxwell's equations symmetry in the terms containing E and B are sought for, and introducing the Maxwell stress-tensor simplifies the result.

Maxwell's equations in SI units in vacuum
(for reference)
Name Differential form
Gauss's law (in vacuum)
Gauss's law for magnetism
Maxwell–Faraday equation
(Faraday's law of induction)
Ampère's circuital law (in vacuum)
(with Maxwell's correction)
  1. Starting with the Lorentz force law
    the force per unit volume for an unknown charge distribution is
    \mathbf{f} = \rho\mathbf{E} + \mathbf{J}\times\mathbf{B}
  2. Next, ρ and J can be replaced by the fields E and B, using Gauss's law and Ampère's circuital law:
    \mathbf{f} = \epsilon_0 \left(\boldsymbol{\nabla}\cdot \mathbf{E} \right)\mathbf{E} + \frac{1}{\mu_0} \left(\boldsymbol{\nabla}\times \mathbf{B} \right) \times \mathbf{B} - \epsilon_0 \frac{\partial \mathbf{E}}{\partial t} \times \mathbf{B}\,
  3. The time derivative can be rewritten to something that can be interpreted physically, namely the Poynting vector. Using the product rule and Faraday's law of induction gives
    and we can now rewrite f as
    ,
    then collecting terms with E and B gives
    \mathbf{f} = \epsilon_0\left + \frac{1}{\mu_0} \left - \epsilon_0\frac{\partial}{\partial t}\left( \mathbf{E}\times \mathbf{B}\right)\,.
  4. A term seems to be "missing" from the symmetry in E and B, which can be achieved by inserting (∇ • B)B because of Gauss' law for magnetism:
    \mathbf{f} = \epsilon_0\left + \frac{1}{\mu_0} \left - \epsilon_0\frac{\partial}{\partial t}\left( \mathbf{E}\times \mathbf{B}\right)\,.
    Eliminating the curls (which are fairly complicated to calculate), using the vector calculus identity
    ,
    leads to:
    \mathbf{f} = \epsilon_0\left + \frac{1}{\mu_0} \left - \frac{1}{2} \boldsymbol{\nabla}\left(\epsilon_0 E^2 + \frac{1}{\mu_0} B^2 \right) - \epsilon_0\frac{\partial}{\partial t}\left( \mathbf{E}\times \mathbf{B}\right)\,.
  5. This expression contains every aspect of electromagnetism and momentum and is relatively easy to compute. It can be written more compactly by introducing the Maxwell stress tensor,
    ,
    and notice that all but the last term of the above can be written as the divergence of this:
    ,
    where we have finally introduced the Poynting vector,
    .

Read more about this topic:  Maxwell Stress Tensor

Famous quotes containing the word motivation:

    “Self-determination has to mean that the leader is your individual gut, and heart, and mind or we’re talking about power, again, and its rather well-known impurities. Who is really going to care whether you live or die and who is going to know the most intimate motivation for your laughter and your tears is the only person to be trusted to speak for you and to decide what you will or will not do.”
    —June Jordan (b. 1939)