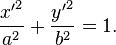Matrix Representation of Conic Sections - Reduced Equation

Reduced Equation

The reduced equation of a conic section is the equation of a conic section translated and rotated so that its center lies in the center of the coordinate system and its axes are parallel to the coordinate axes. This is equivalent to saying that the coordinates are moved to satisfy these properties. See the figure.

If and are the eigenvalues of the matrix A33, the reduced equation can be written as

\lambda_1 x'^2 + \lambda_2 y'^2 + \frac{\det A_Q}{\det A_{33}} = 0

Dividing by we obtain a reduced canonical equation. For example, for an ellipse:

\frac{{x'}^2}{a^2} + \frac{{y'}^2}{b^2} = 1.

From here we get a and b.

The transformation of coordinates is given by:

T: RS(O,X,Y) \mapsto (O'=S,X',Y') \ \stackrel{\mathrm{def}}{=}\ \left\{\begin{align} \vec t &= \overrightarrow {OO'} = S\\ \alpha &= \operatorname{arccos} \frac{\vec a_1 \cdot {1 \choose 0}}{|\vec a_1|} \end{align} \right.

Read more about this topic:  Matrix Representation Of Conic Sections

Famous quotes containing the words reduced and/or equation:

    “The Gettysburg speech is at once the shortest and the most famous oration in American history. Put beside it, all the whoopings of the Websters, Sumners and Everetts seem gaudy and silly. It is eloquence brought to a pellucid and almost gem-like perfection—the highest emotion reduced to a few poetical phrases.”
    —H.L. (Henry Lewis)

    “A nation fights well in proportion to the amount of men and materials it has. And the other equation is that the individual soldier in that army is a more effective soldier the poorer his standard of living has been in the past.”
    —Norman Mailer (b. 1923)