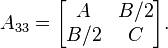Matrix Representation of Conic Sections - Classification

Classification

Regular and degenerated conic sections can be distinguished based on the determinant of A_Q.

If, the conic is degenerate.

If Q is not degenerate, we can see what type of conic section it is by computing the minor (that is, the determinant of the submatrix resulting from removing the last row and the last column of A_Q):

• If and only if, it is a hyperbola.
• If and only if, it is a parabola.
• If and only if, it is an ellipse.

In the case of an ellipse, we can make a further distinction between an ellipse and a circle by comparing the last two diagonal elements corresponding to x2 and y2.

• If and, it is a circle.

Moreover, in the case of a non-degenerate ellipse (with and ), we have a real ellipse if but an imaginary ellipse if . An example of the latter is, which has no real-valued solutions.

If the conic section is degenerate, still allows us to distinguish its form:

• If and only if, it is two intersecting lines.
• If and only if, it is two parallel straight lines. These lines are distinct and real if, coincident if, and distinct and imaginary if .
• If and only if, it is a single point.