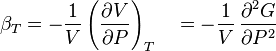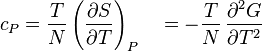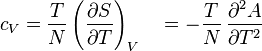Material Properties (thermodynamics)

Material Properties (thermodynamics)

The thermodynamic properties of materials are intensive thermodynamic parameters which are specific to a given material. Each is directly related to a second order differential of a thermodynamic potential. Examples for a simple 1-component system are:

  • Compressibility (or its inverse, the bulk modulus)
  • Isothermal compressibility
\beta_T=-\frac{1}{V}\left(\frac{\partial V}{\partial P}\right)_T \quad = -\frac{1}{V}\,\frac{\partial^2 G}{\partial P^2}
  • Adiabatic compressibility
\beta_S=-\frac{1}{V}\left(\frac{\partial V}{\partial P}\right)_S \quad = -\frac{1}{V}\,\frac{\partial^2 H}{\partial P^2}
  • Specific heat (Note - the extensive analog is the heat capacity)
  • Specific heat at constant pressure
c_P=\frac{T}{N}\left(\frac{\partial S}{\partial T}\right)_P \quad = -\frac{T}{N}\,\frac{\partial^2 G}{\partial T^2}
  • Specific heat at constant volume
c_V=\frac{T}{N}\left(\frac{\partial S}{\partial T}\right)_V \quad = -\frac{T}{N}\,\frac{\partial^2 A}{\partial T^2}
  • Coefficient of thermal expansion
\alpha=\frac{1}{V}\left(\frac{\partial V}{\partial T}\right)_P \quad = \frac{1}{V}\,\frac{\partial^2 G}{\partial P\partial T}

where P is pressure, V is volume, T is temperature, S is entropy, and N is the number of particles.

For a single component system, only three second derivatives are needed in order to derive all others, and so only three material properties are needed to derive all others. For a single component system, the "standard" three parameters are the isothermal compressibility, the specific heat at constant pressure, and the coefficient of thermal expansion .

For example, the following equations are true:

The three "standard" properties are in fact the three possible second derivatives of the Gibbs free energy with respect to temperature and pressure.

Read more about Material Properties (thermodynamics):  Sources

Famous quotes containing the words material and/or properties:

    “A second-class mind dealing with third-class material is hardly a necessity of life.”
    —Harold Laski (1893–1950)

    “A drop of water has the properties of the sea, but cannot exhibit a storm. There is beauty of a concert, as well as of a flute; strength of a host, as well as of a hero.”
    —Ralph Waldo Emerson (1803–1882)