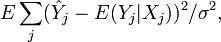Mallows' Cp - Definition and Properties

Definition and Properties

Mallows' Cp addresses the issue of overfitting, in which model selection statistics such as the residual sum of squares always get smaller as more variables are added to a model. Thus, if we aim to select the model giving the smallest residual sum of squares, the model including all variables would always be selected. The Cp statistic calculated on a sample of data estimates the mean squared prediction error (MSPE) as its population target

E\sum_j (\hat{Y}_j - E(Y_j|X_j))^2/\sigma^2,

where is the fitted value from the regression model for the jth case, E(Yj | Xj) is the expected value for the jth case, and σ2 is the error variance (assumed constant across the cases). The MSPE will not automatically get smaller as more variables are added. The optimum model under this criterion is a compromise influenced by the sample size, the effect sizes of the different predictors, and the degree of collinearity between them.

If P regressors are selected from a set of K > P, the Cp statistic for that particular set of regressors is defined as :

where

  • is the error sum of squares for the model with P regressors,
  • Ypi is the predicted value of the i'th observation of Y from the P regressors,
  • S2 is the residual mean square after regression on the complete set of K regressors and can be estimated by mean square error MSE,
  • and N is the sample size.

Read more about this topic:  Mallows' Cp

Famous quotes containing the words definition and/or properties:

    “According to our social pyramid, all men who feel displaced racially, culturally, and/or because of economic hardships will turn on those whom they feel they can order and humiliate, usually women, children, and animals—just as they have been ordered and humiliated by those privileged few who are in power. However, this definition does not explain why there are privileged men who behave this way toward women.”
    —Ana Castillo (b. 1953)

    “A drop of water has the properties of the sea, but cannot exhibit a storm. There is beauty of a concert, as well as of a flute; strength of a host, as well as of a hero.”
    —Ralph Waldo Emerson (1803–1882)