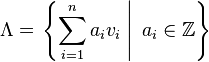Lattice Points - Dividing Space According To A Lattice

Dividing Space According To A Lattice

A typical lattice Λ in thus has the form

$\Lambda = \left.\left\{ \sum_{i=1}^n a_i v_i \; \right\vert \; a_i \in\Bbb{Z} \right\}$

where {v₁, ..., v_n} is a basis for . Different bases can generate the same lattice, but the absolute value of the determinant of the vectors v_i is uniquely determined by Λ, and is denoted by d(Λ). If one thinks of a lattice as dividing the whole of into equal polyhedra (copies of an n-dimensional parallelepiped, known as the fundamental region of the lattice), then d(Λ) is equal to the n-dimensional volume of this polyhedron. This is why d(Λ) is sometimes called the covolume of the lattice.

Read more about this topic: Lattice Points

Famous quotes containing the words dividing and/or space:

“While you are divided from us by geographical lines, which are imaginary, and by a language which is not the same, you have not come to an alien people or land. In the realm of the heart, in the domain of the mind, there are no geographical lines dividing the nations.”
—Anna Howard Shaw (1847–1919)

“... the movie woman’s world is designed to remind us that a woman may live in a mansion, an apartment, or a yurt, but it’s all the same thing because what she really lives in is the body of a woman, and that body is allowed to occupy space only according to the dictates of polite society.”
—Jeanine Basinger (b. 1936)