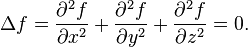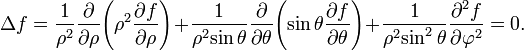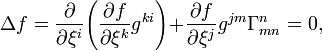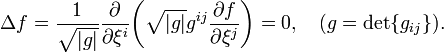Laplace's Equation - Definition

Definition

In three dimensions, the problem is to find twice-differentiable real-valued functions, of real variables x, y, and z, such that

In Cartesian coordinates

$\Delta f = {\partial^2 f\over \partial x^2 } + {\partial^2 f\over \partial y^2 } + {\partial^2 f\over \partial z^2 } = 0.$

In cylindrical coordinates,

$\Delta f = {1 \over r} {\partial \over \partial r} \left( r {\partial f \over \partial r} \right) + {1 \over r^2} {\partial^2 f \over \partial \phi^2} + {\partial^2 f \over \partial z^2 } =0$

In spherical coordinates,

$\Delta f = {1 \over \rho^2}{\partial \over \partial \rho}\!\left(\rho^2 {\partial f \over \partial \rho}\right) \!+\!{1 \over \rho^2\!\sin\theta}{\partial \over \partial \theta}\!\left(\sin\theta {\partial f \over \partial \theta}\right) \!+\!{1 \over \rho^2\!\sin^2\theta}{\partial^2 f \over \partial \varphi^2} =0.$

In Curvilinear coordinates,

$\Delta f = {\partial \over \partial \xi^i}\!\left({\partial f \over \partial \xi^k}g^{ki}\right) \!+\!{\partial f \over \partial \xi^j}g^{jm}\Gamma^n_{mn} =0,$

$\Delta f = {1 \over \sqrt{|g|}}{\partial \over \partial \xi^i}\!\left(\sqrt{|g|}g^{ij}{\partial f \over \partial \xi^j}\right) =0, \quad (g=\mathrm{det}\{g_{ij}\}).$

This is often written as

or, especially in more general contexts,

where ∆ = ∇² is the Laplace operator or "Laplacian"

where ∇ ⋅ = div is the divergence, and ∇ = grad is the gradient.

If the right-hand side is specified as a given function, f(x, y, z), i.e., if the whole equation is written as

then it is called "Poisson's equation".

The Laplace equation is also a special case of the Helmholtz equation.

Read more about this topic: Laplace's Equation

Famous quotes containing the word definition:

“Although there is no universal agreement as to a definition of life, its biological manifestations are generally considered to be organization, metabolism, growth, irritability, adaptation, and reproduction.”
—The Columbia Encyclopedia, Fifth Edition, the first sentence of the article on “life” (based on wording in the First Edition, 1935)

“The very definition of the real becomes: that of which it is possible to give an equivalent reproduction.... The real is not only what can be reproduced, but that which is always already reproduced. The hyperreal.”
—Jean Baudrillard (b. 1929)

“Mothers often are too easily intimidated by their children’s negative reactions...When the child cries or is unhappy, the mother reads this as meaning that she is a failure. This is why it is so important for a mother to know...that the process of growing up involves by definition things that her child is not going to like. Her job is not to create a bed of roses, but to help him learn how to pick his way through the thorns.”
—Elaine Heffner (20th century)