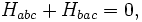Definition
The Lanczos tensor can be defined in a few different ways. The most common modern definition is through the Weyl–Lanczos equations, which demonstrate the generation of the Weyl tensor from the Lanczos tensor. These equations, presented below, were given by Takeno in 1964. The way that Lanczos introduced the tensor originally was as a Lagrange multiplier on constraint terms studied in the variational approach to general relativity. Under any definition, the Lanczos tensor exhibits the following symmetries:
The Lanczos tensor always exists in four dimensions but does not generalize to higher dimensions. This highlights the specialness of four dimensions. Note further that the full Riemann tensor cannot in general be derived from derivatives of the Lanczos potential alone. The Einstein field equations must provide the Ricci tensor to complete the components of the Ricci decomposition.
Read more about this topic: Lanczos Tensor
Famous quotes containing the word definition:
“... we all know the wag’s definition of a philanthropist: a man whose charity increases directly as the square of the distance.”
—George Eliot [Mary Ann (or Marian)
“It is very hard to give a just definition of love. The most we can say of it is this: that in the soul, it is a desire to rule; in the spirit, it is a sympathy; and in the body, it is but a hidden and subtle desire to possess—after many mysteries—what one loves.”
—François, Duc De La Rochefoucauld (1613–1680)