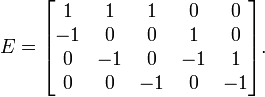Kirchhoff's Theorem - Proof Outline

Proof Outline

First notice that the Laplacian has the property that the sum of its entries across any row and any column is 0. Thus we can transform any minor into any other minor by adding rows and columns, switching them, and multiplying a row or a column by −1. Thus the cofactors are the same up to sign, and it can be verified that, in fact, they have the same sign.

We proceed to show that the determinant of the minor M₁₁ counts the number of spanning trees. Let n be the number of vertices of the graph, and m the number of its edges. The incidence matrix is an n-by-m matrix. Suppose that (i, j) is the kth edge of the graph, and that i < j. Then E_ik = 1, E_jk = −1, and all other entries in column k are 0 (see oriented Incidence matrix for understanding this modified incidence matrix E). For the preceding example (with n = 4 and m = 5):

Recall that the Laplacian L can be factored into the product of the incidence matrix and its transpose, i.e., L = EET. Furthermore, let F be the matrix E with its first row deleted, so that FFT = M₁₁.

Now the Cauchy-Binet formula allows us to write

where S ranges across subsets of of size n − 1, and F_S denotes the (n − 1)-by-(n − 1) matrix whose columns are those of F with index in S. Then every S specifies n − 1 edges of the original graph, and it can be shown that those edges induce a spanning tree iff the determinant of F_S is +1 or −1, and that they do not induce a spanning tree iff the determinant is 0. This completes the proof.