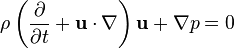Reynolds Number
The assumption of inviscid flow is generally valid where viscous forces are small in comparison to inertial forces. Such flow situations can be identified as flows with a Reynolds number much greater than one. The assumption that viscous forces are negligible can be used to simplify the Navier-Stokes solution to the Euler equations.
The Euler equation governing inviscid flow is:
which is admittedly the Newton's second law applied on a flowing infinitesimal volume element. In the steady-state case, combined with the continuity equation of mass, can be solved using potential flow theory.
Read more about this topic: Inviscid Flow
Famous quotes containing the words reynolds and/or number:
“When Sir Joshua Reynolds died
All Nature was degraded;”
—William Blake (1757–1827)
“Computers are good at swift, accurate computation and at storing great masses of information. The brain, on the other hand, is not as efficient a number cruncher and its memory is often highly fallible; a basic inexactness is built into its design. The brain’s strong point is its flexibility. It is unsurpassed at making shrewd guesses and at grasping the total meaning of information presented to it.”
—Jeremy Campbell (b. 1931)