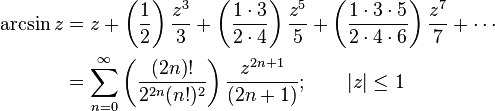Inverse Trigonometric Functions - Infinite Series

Infinite Series

Like the sine and cosine functions, the inverse trigonometric functions can be calculated using infinite series, as follows:

\begin{align} \arcsin z & {}= z + \left( \frac {1} {2} \right) \frac {z^3} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {z^5} {5} + \left( \frac{1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6 } \right) \frac{z^7} {7} + \cdots\\ & {}= \sum_{n=0}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {z^{2n+1}} {(2n+1)} ; \qquad | z | \le 1 \end{align}


\begin{align} \arccos z & {}= \frac {\pi} {2} - \arcsin z \\ & {}= \frac {\pi} {2} - (z + \left( \frac {1} {2} \right) \frac {z^3} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {z^5} {5} + \left( \frac{1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6 } \right) \frac{z^7} {7} + \cdots ) \\ & {}= \frac {\pi} {2} - \sum_{n=0}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {z^{2n+1}} {(2n+1)} ; \qquad | z | \le 1 \end{align}


\begin{align} \arctan z & {}= z - \frac {z^3} {3} +\frac {z^5} {5} -\frac {z^7} {7} +\cdots \\ & {}= \sum_{n=0}^\infty \frac {(-1)^n z^{2n+1}} {2n+1} ; \qquad | z | \le 1 \qquad z \neq i,-i \end{align}


\begin{align} \arccot z & {}= \frac {\pi} {2} - \arctan z \\ & {}= \frac {\pi} {2} - ( z - \frac {z^3} {3} +\frac {z^5} {5} -\frac {z^7} {7} +\cdots ) \\ & {}= \frac {\pi} {2} - \sum_{n=0}^\infty \frac {(-1)^n z^{2n+1}} {2n+1} ; \qquad | z | \le 1 \qquad z \neq i,-i \end{align}


\begin{align} \arcsec z & {}= \arccos {(1/z)} \\ & {}= \frac {\pi} {2} - (z^{-1} + \left( \frac {1} {2} \right) \frac {z^{-3}} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {z^{-5}} {5} + \left( \frac{1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6 } \right) \frac{z^{-7}} {7} + \cdots ) \\ & {}= \frac {\pi} {2} - \sum_{n=0}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {z^{-(2n+1)}} {(2n+1)} ; \qquad \left| z \right| \ge 1 \end{align}


\begin{align} \arccsc z & {}= \arcsin {(1/z)} \\ & {}= z^{-1} + \left( \frac {1} {2} \right) \frac {z^{-3}} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4 } \right) \frac {z^{-5}} {5} + \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {z^{-7}} {7} +\cdots \\ & {}= \sum_{n=0}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {z^{-(2n+1)}} {2n+1} ; \qquad \left| z \right| \ge 1 \end{align}


Leonhard Euler found a more efficient series for the arctangent, which is:

(Notice that the term in the sum for n= 0 is the empty product which is 1.)


Alternatively, this can be expressed:

Read more about this topic:  Inverse Trigonometric Functions

Famous quotes containing the words infinite and/or series:

    “They will visit you at your convenience, whether you are lonesome or not, on rainy days or fair. They propose themselves as either transient acquaintances or permanent friends. They will stay as long as you like, departing or returning as you wish. Their friendship entails no obligation. Best of all, and not always true of our merely human friends, they have Cleopatra’s infinite variety.”
    —Clifton Fadiman (b. 1904)

    “The professional celebrity, male and female, is the crowning result of the star system of a society that makes a fetish of competition. In America, this system is carried to the point where a man who can knock a small white ball into a series of holes in the ground with more efficiency than anyone else thereby gains social access to the President of the United States.”
    —C. Wright Mills (1916–1962)