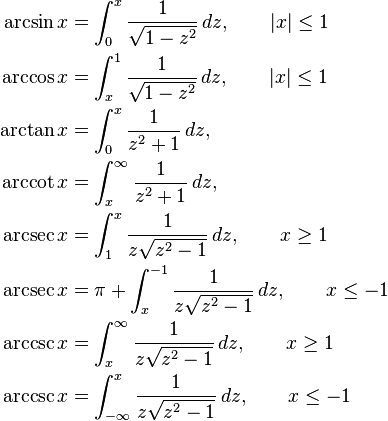Expression As Definite Integrals
Integrating the derivative and fixing the value at one point gives an expression for the inverse trigonometric function as a definite integral:
When x equals 1, the integrals with limited domains are improper integrals, but still well-defined.
Read more about this topic: Inverse Trigonometric Functions
Famous quotes containing the words expression and/or definite:
“Of course, some men are very effective caregivers [of elderly parents]. But this situation occurs far less frequently for males than females, because it is a role reversal. For women, caregiving is an expected duty; for men, it is an unexpected expression of love or devotion.”
—Tish Sommers (20th century)
“The success of a party means little more than that the Nation is using the party for a large and definite purpose.... It seeks to use and interpret a change in its own plans and point of view.”
—Woodrow Wilson (1856–1924)