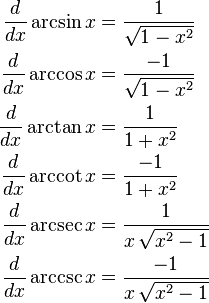Derivatives of Inverse Trigonometric Functions
Simple derivatives for real and complex values of x are as follows:
Only for real values of x:
For a sample derivation: if, we get:
Read more about this topic: Inverse Trigonometric Functions
Famous quotes containing the words inverse and/or functions:
“Yet time and space are but inverse measures of the force of the soul. The spirit sports with time.”
—Ralph Waldo Emerson (1803–1882)
“One of the most highly valued functions of used parents these days is to be the villains of their children’s lives, the people the child blames for any shortcomings or disappointments. But if your identity comes from your parents’ failings, then you remain forever a member of the child generation, stuck and unable to move on to an adulthood in which you identify yourself in terms of what you do, not what has been done to you.”
—Frank Pittman (20th century)