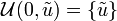Info-gap Decision Theory - Uncertainty Models

Uncertainty Models

Info-gaps are quantified by info-gap models of uncertainty. An info-gap model is an unbounded family of nested sets. For example, a frequently encountered example is a family of nested ellipsoids all having the same shape. The structure of the sets in an info-gap model derives from the information about the uncertainty. In general terms, the structure of an info-gap model of uncertainty is chosen to define the smallest or strictest family of sets whose elements are consistent with the prior information. Since there is, usually, no known worst case, the family of sets may be unbounded.

A common example of an info-gap model is the fractional error model. The best estimate of an uncertain function is, but the fractional error of this estimate is unknown. The following unbounded family of nested sets of functions is a fractional-error info-gap model:

$\mathcal{U}(\alpha, {\tilde{u}}) = \left \{ u(x): \ |u(x) - {\tilde{u}}(x) | \le \alpha {\tilde{u}}(x), \ \mbox{for all}\ x \right \}, \ \ \ \alpha \ge 0$

At any horizon of uncertainty, the set contains all functions whose fractional deviation from is no greater than . However, the horizon of uncertainty is unknown, so the info-gap model is an unbounded family of sets, and there is no worst case or greatest deviation.

There are many other types of info-gap models of uncertainty. All info-gap models obey two basic axioms:

Nesting. The info-gap model is nested if implies that:

$\mathcal{U}(\alpha, {\tilde{u}}) \ \subseteq \ \mathcal{U}(\alpha^\prime, {\tilde{u}})$

Contraction. The info-gap model is a singleton set containing its center point:

$\mathcal{U}(0,{\tilde{u}}) = \{ {\tilde{u}} \}$

The nesting axiom imposes the property of "clustering" which is characteristic of info-gap uncertainty. Furthermore, the nesting axiom implies that the uncertainty sets become more inclusive as grows, thus endowing with its meaning as an horizon of uncertainty. The contraction axiom implies that, at horizon of uncertainty zero, the estimate is correct.

Recall that the uncertain element may be a parameter, vector, function or set. The info-gap model is then an unbounded family of nested sets of parameters, vectors, functions or sets.

Read more about this topic: Info-gap Decision Theory

Famous quotes containing the words uncertainty and/or models:

“Now, since our condition accommodates things to itself, and transforms them according to itself, we no longer know things in their reality; for nothing comes to us that is not altered and falsified by our Senses. When the compass, the square, and the rule are untrue, all the calculations drawn from them, all the buildings erected by their measure, are of necessity also defective and out of plumb. The uncertainty of our senses renders uncertain everything that they produce.”
—Michel de Montaigne (1533–1592)

“Today it is not the classroom nor the classics which are the repositories of models of eloquence, but the ad agencies.”
—Marshall McLuhan (1911–1980)