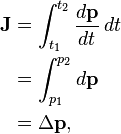Impulse (physics) - Mathematical Derivation in The Case of An Object of Constant Mass | Mathematical Derivation Case Object Constant Mass

Mathematical Derivation in The Case of An Object of Constant Mass

Impulse J produced from time t₁ to t₂ is defined to be

where F is the force applied from t₁ to t₂.

From Newton's second law, force is related to momentum p by

Therefore

$\begin{align} \mathbf{J} &= \int_{t_1}^{t_2} \frac{d\mathbf{p}}{dt}\, dt \\ &= \int_{p_1}^{p_2} d\mathbf{p} \\ &= \Delta \mathbf{p}, \end{align}$

where Δp is the change in momentum from time t₁ to t₂. This is often called the impulse-momentum theorem.

As a result, an impulse may also be regarded as the change in momentum of an object to which a force is applied. The impulse may be expressed in a simpler form when both the force and the mass are constant:

It is often the case that not just one but both of these two quantities vary.

In the technical sense, impulse is a physical quantity, not an event or force. The term "impulse" is also used to refer to a fast-acting force. This type of impulse is often idealized so that the change in momentum produced by the force happens with no change in time. This sort of change is a step change, and is not physically possible. This is a useful model for computing the effects of ideal collisions (such as in game physics engines).

Impulse has the same units (in the International System of Units, kg·m/s = N·s) and dimensions (M L T−1) as momentum.

Impulse can be calculated using the equation

where

F is the constant total net force applied,

t is the time interval over which the force is applied,

m is the constant mass of the object,

v₁ is the final velocity of the object at the end of the time interval, and

v₀ is the initial velocity of the object when the time interval begins.

Read more about this topic: Impulse (physics)

Famous quotes containing the words mathematical, case, object, constant and/or mass:

“An accurate charting of the American woman’s progress through history might look more like a corkscrew tilted slightly to one side, its loops inching closer to the line of freedom with the passage of time—but like a mathematical curve approaching infinity, never touching its goal. . . . Each time, the spiral turns her back just short of the finish line.”
—Susan Faludi (20th century)

“... business training in early life should not be regarded solely as insurance against destitution in the case of an emergency. For from business experience women can gain, too, knowledge of the world and of human beings, which should be of immeasurable value to their marriage careers. Self-discipline, co-operation, adaptability, efficiency, economic management,—if she learns these in her business life she is liable for many less heartbreaks and disappointments in her married life.”
—Hortense Odlum (1892–?)

“I felt more determined than ever to become a physician, and thus place a strong barrier between me and all ordinary marriage. I must have something to engross my thoughts, some object in life which will fill this vacuum and prevent this sad wearing away of the heart.”
—Elizabeth Blackwell (1821–1910)

“Our kindred, though they be long ere they be wooed, they are constant being won; they are burrs, I can tell you, they’ll stick where they are thrown.”
—William Shakespeare (1564–1616)

“No man’s thoughts are new, but the style of their expression is the never-failing novelty which cheers and refreshes men. If we were to answer the question, whether the mass of men, as we know them, talk as the standard authors and reviewers write, or rather as this man writes, we should say that he alone begins to write their language at all.”
—Henry David Thoreau (1817–1862)