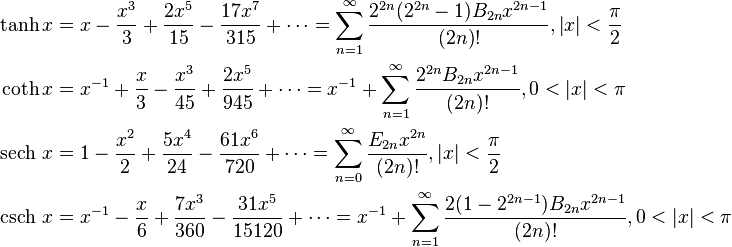Hyperbolic Function - Taylor Series Expressions

Taylor Series Expressions

It is possible to express the above functions as Taylor series:

The function sinh x has a Taylor series expression with only odd exponents for x. Thus it is an odd function, that is, −sinh x = sinh(−x), and sinh 0 = 0.

The function cosh x has a Taylor series expression with only even exponents for x. Thus it is an even function, that is, symmetric with respect to the y-axis. The sum of the sinh and cosh series is the infinite series expression of the exponential function.

\begin{align} \tanh x &= x - \frac {x^3} {3} + \frac {2x^5} {15} - \frac {17x^7} {315} + \cdots = \sum_{n=1}^\infty \frac{2^{2n}(2^{2n}-1)B_{2n} x^{2n-1}}{(2n)!}, \left |x \right | < \frac {\pi} {2} \\ \coth x &= x^{-1} + \frac {x} {3} - \frac {x^3} {45} + \frac {2x^5} {945} + \cdots = x^{-1} + \sum_{n=1}^\infty \frac{2^{2n} B_{2n} x^{2n-1}} {(2n)!}, 0 < \left |x \right | < \pi \\ \operatorname {sech}\, x &= 1 - \frac {x^2} {2} + \frac {5x^4} {24} - \frac {61x^6} {720} + \cdots = \sum_{n=0}^\infty \frac{E_{2 n} x^{2n}}{(2n)!}, \left |x \right | < \frac {\pi} {2} \\ \operatorname {csch}\, x &= x^{-1} - \frac {x} {6} +\frac {7x^3} {360} -\frac {31x^5} {15120} + \cdots = x^{-1} + \sum_{n=1}^\infty \frac{ 2 (1-2^{2n-1}) B_{2n} x^{2n-1}}{(2n)!}, 0 < \left |x \right | < \pi \end{align}

where

is the nth Bernoulli number
is the nth Euler number

Read more about this topic:  Hyperbolic Function

Famous quotes containing the words taylor, series and/or expressions:

    “To be beloved is all I need,
    And whom I love, I love indeed.”
    —Samuel Taylor Coleridge (1772–1834)

    “Life ... is not simply a series of exciting new ventures. The future is not always a whole new ball game. There tends to be unfinished business. One trails all sorts of things around with one, things that simply won’t be got rid of.”
    —Anita Brookner (b. 1928)

    “Compare the history of the novel to that of rock ‘n’ roll. Both started out a minority taste, became a mass taste, and then splintered into several subgenres. Both have been the typical cultural expressions of classes and epochs. Both started out aggressively fighting for their share of attention, novels attacking the drama, the tract, and the poem, rock attacking jazz and pop and rolling over classical music.”
    —W. T. Lhamon, U.S. educator, critic. “Material Differences,” Deliberate Speed: The Origins of a Cultural Style in the American 1950s, Smithsonian (1990)