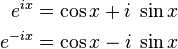Hyperbolic Functions For Complex Numbers
Since the exponential function can be defined for any complex argument, we can extend the definitions of the hyperbolic functions also to complex arguments. The functions sinh z and cosh z are then holomorphic.
Relationships to ordinary trigonometric functions are given by Euler's formula for complex numbers:
so:
Thus, hyperbolic functions are periodic with respect to the imaginary component, with period ( for hyperbolic tangent and cotangent).
Read more about this topic: Hyperbolic Function
Famous quotes containing the words functions, complex and/or numbers:
“The English masses are lovable: they are kind, decent, tolerant, practical and not stupid. The tragedy is that there are too many of them, and that they are aimless, having outgrown the servile functions for which they were encouraged to multiply. One day these huge crowds will have to seize power because there will be nothing else for them to do, and yet they neither demand power nor are ready to make use of it; they will learn only to be bored in a new way.”
—Cyril Connolly (1903–1974)
“All propaganda or popularization involves a putting of the complex into the simple, but such a move is instantly deconstructive. For if the complex can be put into the simple, then it cannot be as complex as it seemed in the first place; and if the simple can be an adequate medium of such complexity, then it cannot after all be as simple as all that.”
—Terry Eagleton (b. 1943)
“The forward Youth that would appear
Must now forsake his Muses dear,
Nor in the Shadows sing
His Numbers languishing.”
—Andrew Marvell (1621–1678)