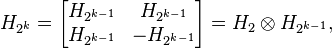Hadamard Matrix - Sylvester's Construction

Sylvester's Construction

Examples of Hadamard matrices were actually first constructed by James Joseph Sylvester in 1867. Let H be a Hadamard matrix of order n. Then the partitioned matrix

is a Hadamard matrix of order 2n. This observation can be applied repeatedly and leads to the following sequence of matrices, also called Walsh matrices.

$H_1 = \begin{bmatrix} 1 \end{bmatrix},$

$H_2 = \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix},$

and

$H_{2^k} = \begin{bmatrix} H_{2^{k-1}} & H_{2^{k-1}}\\ H_{2^{k-1}} & -H_{2^{k-1}}\end{bmatrix} = H_2\otimes H_{2^{k-1}},$

for, where denotes the Kronecker product.

In this manner, Sylvester constructed Hadamard matrices of order 2k for every non-negative integer k.

Sylvester's matrices have a number of special properties. They are symmetric and have trace zero. The elements in the first column and the first row are all positive. The elements in all the other rows and columns are evenly divided between positive and negative. Sylvester matrices are closely connected with Walsh functions.

Read more about this topic: Hadamard Matrix

Famous quotes containing the words sylvester and/or construction:

“With deep affection and recollection
I often think of the Shandon bells,”
—Francis Sylvester Mahony (1805–1866)

“No real “vital” character in fiction is altogether a conscious construction of the author. On the contrary, it may be a sort of parasitic growth upon the author’s personality, developing by internal necessity as much as by external addition.”
—T.S. (Thomas Stearns)