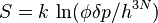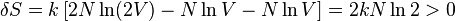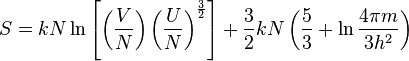Gibbs Paradox - Calculating The Entropy of Ideal Gas, and Making IT Extensive

Calculating The Entropy of Ideal Gas, and Making It Extensive

In classical mechanics, the state of an ideal gas of energy U, volume V and with N particles, each particle having mass m, is represented by specifying the momentum vector p and the position vector x for each particle. This can be thought of as specifying a point in a 6N-dimensional phase space, where each of the axes corresponds to one of the momentum or position coordinates of one of the particles. The set of points in phase space that the gas could occupy is specified by the constraint that the gas will have a particular energy:

and be contained inside of the volume V (let's say V is a box of side X so that V=X3):

for : and

The first constraint defines the surface of a 3N-dimensional hypersphere of radius (2mU)1/2 and the second is a 3N-dimensional hypercube of volume VN. These combine to form a 6N-dimensional hypercylinder. Just as the area of the wall of a cylinder is the circumference of the base times the height, so the area φ of the wall of this hypercylinder is:

\phi(U,V,N) = V^N \left(\frac{2\pi^{\frac{3N}{2}}(2mU)^{\frac{3N-1}{2}}}{\Gamma(3N/2)}\right)~~~~~~~~~~~(1)

The entropy is proportional to the logarithm of the number of states that the gas could have while satisfying these constraints. In classical physics, the number of states is infinitely large, but according to quantum mechanics it is finite. Before the advent of quantum mechanics, this infinity was regularized by making phase space discrete. Phase space was divided up in blocks of volume . The constant h thus appeared as a result of a mathematical trick and thought to have no physical significance. However, using quantum mechanics one recovers the same formalism in the semi-classical limit, but now with h being Planck's constant. One can qualitatively see this from Heisenberg's uncertainty principle; a volume in N phase space smaller than h3N (h is Planck's constant) cannot be specified.

To compute the number of states we must compute the volume in phase space in which the system can be found and divide that by . This leads us to another problem: The volume seems to approach zero, as the region in phase space in which the system can be is an area of zero thickness. This problem is an artifact of having specified the energy U with infinite accuracy. In a generic system without symmetries, a full quantum treatment would yield a discrete non-degenerate set of energy eigenstates. An exact specification of the energy would then fix the precise state the system is in, so the number of states available to the system would be one, the entropy would thus be zero.

When we specify the internal energy to be U, what we really mean is that the total energy of the gas lies somewhere in an interval of length around U. Here is taken to be very small, it turns out that the entropy doesn't depend strongly on the choice of for large N. This means that the above "area" must be extended to a shell of a thickness equal to an uncertainty in momentum, so the entropy is given by:

\left.\right. S=k\,\ln(\phi \delta p/h^{3N})

where the constant of proportionality is k, Boltzmann's constant. Using Stirling's approximation for the Gamma function which omits terms of less than order N, the entropy for large N becomes:

S = k N \ln \left+ {\frac 32}kN\left( 1+ \ln\frac{4\pi m}{3h^2}\right)

This quantity is not extensive as can be seen by considering two identical volumes with the same particle number and the same energy. Suppose the two volumes are separated by a barrier in the beginning. Removing or reinserting the wall is reversible, but the entropy difference after removing the barrier is

\delta S = k \left = 2 k N \ln 2 > 0

which is in contradiction to thermodynamics. This is the Gibbs paradox.

The paradox is resolved by postulating that the gas particles are in fact indistinguishable. This means that all states that differ only by a permutation of particles should be considered as the same state. For example, if we have a 2-particle gas and we specify AB as a state of the gas where the first particle (A) has momentum p1 and the second particle (B) has momentum p2, then this state as well as the BA state where the B particle has momentum p1 and the A particle has momentum p2 should be counted as the same state.

For an N-particle gas, there are N! states which are identical in this sense, if one assumes that each particle is in a different single particle state. One can safely make this assumption provided the gas isn't at an extremely high density. Under normal conditions, one can thus calculate the volume of phase space occupied by the gas, by dividing Equation 1 by N!. Using the Stirling approximation again for large N, ln(N!) ≈ N ln(N) - N, the entropy for large N is:

S = k N \ln \left+ {\frac 32}kN\left( {\frac 53}+ \ln\frac{4\pi m}{3h^2}\right)

which can be easily shown to be extensive. This is the Sackur-Tetrode equation.

Read more about this topic:  Gibbs Paradox

Famous quotes containing the words calculating the, calculating, entropy, ideal, making and/or extensive:

    “[The] elderly and timid single gentleman in Paris ... never drove down the Champs Elysees without expecting an accident, and commonly witnessing one; or found himself in the neighborhood of an official without calculating the chances of a bomb. So long as the rates of progress held good, these bombs would double in force and number every ten years.”
    —Henry Brooks Adams (1838–1918)

    “What our children have to fear is not the cars on the highways of tomorrow but our own pleasure in calculating the most elegant parameters of their deaths.”
    —J.G. (James Graham)

    “Just as the constant increase of entropy is the basic law of the universe, so it is the basic law of life to be ever more highly structured and to struggle against entropy.”
    —Václav Havel (b. 1936)

    “The ideal of men and women sharing equally in parenting and working is a vision still. What would it be like if women and men were less different from each other, if our worlds were not so foreign? A male friend who shares daily parenting told me that he knows at his very core what his wife’s loving for their daughter feels like, and that this knowing creates a stronger bond between them.”
    —Anonymous Mother. Ourselves and Our Children, by Boston Women’s Health Book Collective, ch. 6 (1978)

    “That excitement about Kossuth, consider how characteristic, but superficial, it was!—only another kind of politics or dancing. Men were making speeches to him all over the country, but each expressed only the thought, or the want of thought, of the multitude. No man stood on truth. They were merely banded together, as usual one leaning on another, and all together on nothing.”
    —Henry David Thoreau (1817–1862)

    “We have all heard of Young America. He is the most current youth of the age.
    Some think him conceited, and arrogant; but has he not reason to entertain a rather extensive opinion of himself? Is he not the inventor and owner of the present, and sole hope of the future?”
    —Abraham Lincoln (1809–1865)