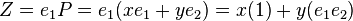Relationship With Other Formalisms
may be directly compared to vector algebra.
The even subalgebra of is isomorphic to the complex numbers, as may be seen by writing a vector P in terms of its components in an orthonormal basis and left multiplying by the basis vector e1, yielding
where we identify i ↦ e1e2 since
Similarly, the even subalgebra of with basis {1, e2e3, e3e1, e1e2} is isomorphic to the quaternions as may be seen by identifying i ↦ −e2e3, j ↦ −e3e1 and k ↦ −e1e2.
Every associative algebra has a matrix representation; the Pauli matrices are a representation of and the Dirac matrices are a representation of, showing the equivalence with matrix representations used by physicists.
Read more about this topic: Geometric Algebra
Famous quotes containing the words relationship with and/or relationship:
“Henry David Thoreau, who never earned much of a living or sustained a relationship with any woman that wasn’t brotherly—who lived mostly under his parents’ roof ... who advocated one day’s work and six days “off” as the weekly round and was considered a bit of a fool in his hometown ... is probably the American writer who tells us best how to live comfortably with our most constant companion, ourselves.”
—Edward Hoagland (b. 1932)
“The relationship between mother and professional has not been a partnership in which both work together on behalf of the child, in which the expert helps the mother achieve her own goals for her child. Instead, professionals often behave as if they alone are advocates for the child; as if they are the guardians of the child’s needs; as if the mother left to her own devices will surely damage the child and only the professional can rescue him.”
—Elaine Heffner (20th century)